Assalamu‘alaikum wr. wb.
Halo gais, Kembali lagi bersama Inzaghi's Blog! Jika sebelumnya kita sudah membuatkan Tutorial Ms. Excel beserta Tabel Distribusi dan Analisis Deskriptif. Sekarang, waktunya kita akan memberikan Rumus-rumus Regresi Linier dan Korelasi beserta dengan Tutorial pembuatannya di SPSS.
PENGERTIAN DAN RUMUS
Sumber Artikel Materi : Statistikian.com
A. Analisis Regresi Linear
Analisis regresi mempelajari bentuk hubungan antara satu atau lebih peubah/variabel bebas (X) dengan satu Peubah Tak Bebas (Y). Dalam penelitian Peubah Bebas (X) biasanya peubah yang ditentukan oleh peneliti secara bebas misalnya dosis obat, lama penyimpanan, kadar zat pengawet, umur ternak dan sebagainya.
Di samping itu peubah bebas bisa juga berupa peubah tak bebasnya, misalnya dalam pengukuran panjang badan dan berat badan sapi, karena panjang badan lebih mudah diukur maka panjang badan dimasukkan kedalam Peubah Bebas (X), sedangkan berat badan dimasukkan Peubah Tak Bebas (Y).
Sedangkan peubah tak bebas (Y) dalam penelitian berupa respon yang diukur akibat perlakuan/peubah bebas (X). misalnya jumlah sel darah merah akibat pengobatan dengan dosis tertentu, jumlah mikroba daging setelah disimpan beberapa hari, berat ayam pada umur tertentu dan sebagainya.
B. Tujuan Regresi Linear
Regresi linier adalah salah satu dari jenis analisis peramalan atau prediksi yang sering digunakan pada data berskala kuantitatif (interval atau rasio).
Tujuan dilakukannya regresi linear antara lain adalah :
- Apakah seperangkat atau sekumpulan variabel prediktor signifikan dalam memprediksi variabel respon?
- Variabel predictor manakah yang signifikan dalam menjelaskan variable respon? Hal ini ditunjukkan dengan koefisien estimasi regresi. Koefisien estimasi inilah yang nantinya akan membentuk persamaan regresi.
C. Bentuk Hubungan Variabel Bebas dan Terikat
Bentuk hubungan antara peubah bebas (X) dengan peubah tak bebas (Y) bisa dalam bentuk polinom derajat satu (linear) polinom derajat dua (kuadratik). Polinom derajat tiga (Kubik) dan seterusnya. Disamping itu bisa juga dalam bentuk lain misalnya eksponensial, logaritma, sigmoid dan sebagainya. Bentuk-bentuk ini dalam analisis regresi-korelasi biasanya dilakukan transformasi supaya menjadi bentuk polinom.
D. Persamaan dan Contoh Regresi
Dalam bentuk yang paling sederhana yaitu satu peubah bebas (X) dengan satu peubah tak bebas (Y) mempunyai persamaan :
Persamaan Regresi sederhana :
Keterangan :
Y = Nilai yang diramalkan
a = Konstanta
b = Koefisien regresi
X = Variabel bebas
ε = Nilai Residu
1. Contoh Persamaan Regresi
Sebagai contoh misalnya titik A (1,3) dan titik B (1,9) maka persamaan garis linear yang dapat dibuat adalah :
Dalam bentuk Matriks bisa kita buat Persamaan sebagai berikut :
Jadi a = 1 dan b = 2 sehingga persamaannya Y = 1+2X
Jika jumlah data sebanyak n maka persamaannya sebagai berikut :
i = 1, 2, 3, 4, ..., n
Disini β0 adalah penduga a, β1 adlah penduga b dan εi merupakan besarnya simpangan persamaan garis penduga. Semakin kecil nilai εi persamaan regresi yang diperoleh akan semakin baik.
Penulisan Pengamatan
Jadi kita dapat menuliskan pengamatan kita menjadi:
Dengan notasi matriks dapat ditulis sebagai berikut :
Jadi kita peroleh matrik Y,X,β dan ε dengan dimensi sebagai berikut :
Jika diasumsikan E(ε) = 0 maka E(Y) = Xβ
Bila modelnya benar β merupakan penduga terbaik yaitu dengan jalan melakukan penggandaan awal dengan X’ sehingga diperoleh persamaan normal sebagai berikut:
Jadi β = (X’X)-1X’Y
Di sini, (X’X)-1 adalah kebalikan (inverse) dari matrik X’X
2. Contoh Perhitungan Regresi
Seorang peneliti ingin mengetahui bentuk hubungan antara jumlah cacing jenis tertentu dengan jumlah telurnya pada Usus Ayam Buras. Untuk tujuan tersebut diperiksa 20 ekor ayam dan ditemukan sebagai berikut :
Tabel Jumlah Cacing dan Jumlah Telur pada Usus Ayam Buras.
Dari data diatas kita bisa menghitung :
Bila kita duga bentuk hubungan antara jumlah cacing (X) dan jumlah telurnya (Y) adalah :
Jadi Ŷ=-2,442 + 4,103 Xi
Persamaan Garis regresi Banyak Jenisnya
Persamaan garis regresi Yi =-2,442 + 4,103 Xi bukanlah satu-satunya garis penduga untuk menyatakan hubungan antara jumlah cacing dengan jumlah telurnya. Sudah barang tentu masih banyak lagi bentuk persamaan penduga yang dapat dibuat misalnya dalam bentuk persamaan Yi=βo+β1Xi+β2Xi2,Yi=βoXiβ1 (dalam bentuk linear LnYi=Ln βo+βiLnXi) dan masih banyak lagi bentuk yang lainnya.
Untuk menyatakan apakah garis yang diperoleh cukup baik untuk menggambarkan hubungan antara peubah bebas (X) dengan peubah tak bebas (Y) dapat dilakukan pengujian bentuk model yang digunakan dan keeratan hubungannya (korelasi) untuk menyatakan ketepatan dan ketelitian persamaan garis regresi yang diperoleh.
E. Teori dan Kriteria Pengujian Korelasi
Sumber : Tambahpinter.com
Uji Korelasi merupakan salah satu uji statistik yang digunakan untuk mengetahui keeratan hubungan variabel bebas dan variabel tidak bebas.
Uji korelasi merupakan pengujian atau analisis data yang berfungsi untuk mengetahui tingkat keeratan hubungan antara variabel bebas (X) dan variabel tidak bebas (Y). Dalam uji ini, pengujiannya hanya untuk mengetahui hubungannya saja. Bentuk hubungan yang dimaksud adalah mengetahui sifat hubungan variabel X dan Y, bentuknya yaitu :
- Apabila sifat hubungannya positif, artinya jika variabel X naik, maka variabel Y juga naik.
- Apabila sifat hubungannya negatif, artinya jika variabel X naik, maka variabel Y turun. Jadi, kebalikannya atau memiliki arah yang berlawanan.
- Apabila kedua variabel tidak memiliki hubungan, maka nilainya akan menunjukkan angka 0 (nol).
Dalam setiap pengujian statistik pasti memiliki syarat atau kriteria pengujian yang digunakan untuk menginterpretasikan atau menjabarkan arti dari nilai-nilai yang diperoleh saat pengujian. Dalam uji korelasi terdapat tiga cara untuk mengetahui hubungan antara variabel X dan Y, yaitu :
- Melihat dari rhitung, caranya dengan membandingkan rhitung dengan rtabel. Apabila rhitung > rtabel maka H0 ditolak artinya kedua variabel memiliki hubungan. Apabila rhitung < rtabel maka H0 diterima artinya kedua variabel tidak memiliki hubungan.
- Melihat dari nilai signifikansinya. Caranya apabila nilai signifikansi variabel < 0,05 artinya terdapat hubungan secara signifikan antara kedua variabel. Apabila > 0,05 artinya tidak terdapat hubungan secara signifikan antara kedua variabel.
- Melihat nilai Pearson Correlation. Apabila nilainya sama dengan 0 (nol), maka kedua variabel tidak terdapat hubungan. Sebaliknya, Apabila nilainya tidak sama dengan 0 (nol), maka kedua variabel terdapat hubungan.
TUTORIAL REGRESI DAN KORELASI SPSS
Sumber Artikel Materi : Statistikian.com (Regresi Linear Sederhana)
Analisis regresi linear sederhana merupakan salah satu metode regresi yang dapat dipakai sebagai alat inferensi statistik untuk menentukan pengaruh sebuah variabel bebas (independen) terhadap variabel terikat (dependen). Uji Regresi linear sederhana ataupun regresi linier berganda pada intinya memiliki beberapa tujuan, yaitu :
- Menghitung nilai Estimasi rata-rata dan nilai variabel terikat berdasarkan pada nilai variabel bebas.
- Menguji hipotesis karakteristik dependensi
- Meramalkan nilai rata-rata variabel bebas dengan didasarkan pada nilai variabel bebas di luar jangkauan sample.
Pada analisis regresi sederhana dengan menggunakan SPSS ada beberapa asumsi dan persyaratan yang perlu diperiksa dan diuji, beberapa di antaranya adalah :
- Variabel bebas tidak berkorelasi dengan disturbance term (Error). Nilai disturbance tersebar 0 atau dengan simbol sebagai berikut: E (U / X) = 0,
- Jika variabel bebas lebih dari satu, maka antara variabel bebas (explanatory) tidak ada hubungan linier yang nyata,
- Model regresi dikatakan layak jika angka signifikansi pada ANOVA sebesar < 0.05, Predictor yang digunakan sebagai variabel bebas harus layak. Kelayakan ini diketahui jika angka Standard Error of Estimate < Standard Deviation,
- Koefisien regresi harus signifikan. Pengujian dilakukan dengan Uji T. Koefisien regresi signifikan jika T hitung > T table (nilai kritis),
- Model regresi dapat diterangkan dengan menggunakan nilai koefisien determinasi (KD = R Square x 100%) semakin besar nilai tersebut maka model semakin baik. Jika nilai mendekati 1 maka model regresi semakin baik,
- Residual harus terdistribusi normal,
- Data berskala interval atau rasio,
- Kedua variabel bersifat dependen, artinya satu variabel merupakan variabel bebas (variabel predictor) sedang variabel lainnya variabel terikat (variabel response) Berikut ini contoh perhitungan regresi linier sederhana menggunakan Software SPSS versi 20 keatas.
A. Membuat Tabel Regresi di Excel dan SPSS
Dan inilah Tutorial Regresi Linear Sederhana dengan SPSS.
1. Tentukan Judul Regresi
Pertama, tentukan terlebih dahulu Judul dari Regresi Linear. Misalnya, Pengaruh .... terhadap .... untuk judulnya. Sebenarnya bisa saja tanpa Judul, hanya saja kita harus menggunakan Variabel X dan Y. Sebagai contohnya, "Pengaruh terhadap Volume Perusahaan-perusahaan di Kota Tangerang".
2. Buat Tabel Data di Excel
Selanjutnya, Buat Tabel Data terlebih dahulu di Excel. Misalnya, pada Kasus diatas bahwa Promosi akan menjadi variabel x dan juga Volume sebagai variabel y. Untuk jumlah datanya, kita bisa asal mengisi sampai 100 Data secara Acak dengan menggunakan Rumus Excel =RANDBETWEEN(terendah; tertinggi). Akan seperti ini jadinya :
3. Buka, Salin, dan Tempelkan ke SPSS
Selanjutnya, kita Copy semua Tabel Sheets di Excel lalu kita Tempelkan (Paste) ke SPSS dengan mengeklik "Paste with Variable Names".
Selanjutnya, kita ubah Pecahan Desimal-nya menjadi 0 dengan mengeklik di bagian "Variable View" di Pojok Bawah.
Selanjutnya, kita klik pada menu "Analyze" lalu pilih "Regression --> Linear...".
Kemudian, pilih Variabel Y (Volume) sebagai Variabel Dependen (Terikat) dan X (Promosi) sebagai Variabel Independen (Bebas) lalu klik Tombol "OK".
Jika sudah selesai, maka hasilnya akan seperti ini :
Output SPSS akan menampilkan hasil berupa 4 Buah tabel yaitu :
- Tabel Variabel Penelitian
- Ringkasan Model (Model Summary)
- Tabel ANOVA
- Tabel Koefisien
5. Hasil Regresi dengan SPSS
- Tabel pertama menunjukkan variabel apa saja yang diproses, mana yang menjadi variabel bebas dan variabel terikat.
- Tabel kedua menampilkan nilai R yang merupakan simbol dari nilai koefisien korelasi. Pada contoh diatas nilai korelasi adalah 0,031. Nilai ini dapat diinterpretasikan bahwa hubungan kedua variabel penelitian ada di kategori lemah. Melalui tabel ini juga diperoleh nilai R Square atau koefisien determinasi (KD) yang menunjukkan seberapa bagus model regresi yang dibentuk oleh interaksi variabel bebas dan variabel terikat. Nilai KD yang diperoleh adalah 0,1% yang dapat ditafsirkan bahwa variabel bebas X1 memiliki pengaruh kontribusi sebesar 0,1% terhadap variabel Y dan 99,9% lainnya dipengaruhi oleh faktor-faktor lain di luar variabel X1.
- Tabel ketiga digunakan untuk menentukan Taraf Signifikansi atau Linearitas dari regresi. Kriterianya dapat ditentukan berdasarkan Uji F atau Uji nilai Signifikansi (Sig.). Cara yang paling mudah dengan uji Sig., dengan ketentuan, jika Nilai Sig. < 0,05, maka model regresi adalah linier, dan berlaku sebaliknya. Berdasarkan tabel ketiga, diperoleh nilai Sig. = 0,762 yang berarti > kriteria signifikan (0,05), dengan demikian model persamaan regresi berdasarkan data penelitian adalah tidak signifikan artinya, model regresi linier tidak memenuhi kriteria Linearitas.
- Tabel keempat menginformasikan model persamaan regresi yang diperoleh dengan koefisien konstanta dan koefisien variabel yang ada di kolom Unstandardized Coefficients B. Berdasarkan tabel ini diperoleh model persamaan regresi : Y = 52,275 - 0,029 X1.
Video Tutorial Regresi Linear Sederhana SPSS di YouTube :
B. Membuat Korelasi di SPSS
Sumber : Tambahpinter.com dan Statistikian.com (Korelasi)
Anda kemudian akan mempelajari cara menguji korelasi Pearson menggunakan aplikasi SPSS. Sebelum memulai silakan siapkan Data yang ingin dicek terlebih dahulu, bisa menggunakan Data yang diatas (Korelasi).
1. Mengatur Korelasi menggunakan SPSS
Caranya sama seperti di atas untuk melakukan Copy-Paste Data ke SPSS, dan aturlah Bilangan Desimal di bagian "Variable View". Selanjutnya, kita klik pada menu "Analyze" lalu pilih "Correlate --> Bivariate...".
Maka akan muncul kotak dialog. Lalu, pindahkan Variabel X (Promosi) dan Y (Volume) ke kotak "Variables". Pada "Correlation Coefficients", centanglah pada "Pearson". Pada "Test of Significance", centanglah "Two-tailed", dan terakhir centang "Flag significant correlations". Lalu, klik pada Tombol "OK".
Dan inilah Hasil Korelasi yang diperoleh dengan menggunakan SPSS :
C. Analisis dari Hasil Korelasi di SPSS
1. Membandingkan rhitung dengan r
Pertama, mencari nilai rtabel terlebih dulu. Sesuaikan dengan ketentuan df(N-2, 0,05). ‘N’ merupakan jumlah data sampel yang diuji. Setelah dimasukkan ke rumus, lalu mencari nilai rtabel di data tabel r.
 |
| Selanjutnya, dapat di-Download di sini untuk Tabel R |
rtabel = df(100-2, 0.05) = df(98, 0.05) = 0,165
Kedua, bandingkan rhitung dengan rtabel lalu interpretasikan sesuai kriteria pengujian.
Diketahui rhitung = -0,031 dan rtabel = 0,165.
-0,031 < 0,165 maka H0 ditolak artinya antara variabel X dan Y tidak terdapat hubungan positif.
2. Melihat Nilai Signifikansinya
Diketahui nilai signifikansi (2-tailed) sebesar 0,762.
0,762 > 0,05 artinya antara variabel X dan Y tidak terdapat hubungan yang signifikan.
Uji Korelasi merupakan uji statistik yang hanya untuk mengetahui apakah ada hubungan antara dua variabel atau lebih dari penelitian atau seberapa besar hubungan antar variabel penelitian. Dari penjelasan diatas, kamu sekarang sudah bagaimana teori, cara pengujian, kriteria pengujian dan interpretasi dari Uji Korelasi.
Semoga bermanfaat bagi Mahasiswa, jika ingin mengunduh (Download) SPSS secara Gratis, silakan klik di sini (Google Drive). Dan jika ingin melihat dan mengunduh (Download) File Excel Tabel Distribusi Z, T, dan F, silakan lihat di sini. Dan untuk mengunduh (Download) Tabel R, silakan lihat di sini.
Terima Kasih 😄😘👌👍 :)
Wassalamu‘alaikum wr. wb.

.png)


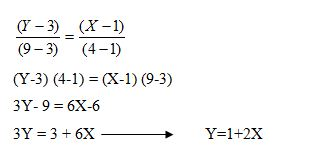









.jpg)
%20di%20SPSS.jpg)

%20(2).jpg)
.jpg)

.jpg)
.jpg)


