Assalamu‘alaikum wr. wb.
Hello guys! Apakah Anda tahu tentang Ordinal dan Kardinal? Biasanya kalian hanya mengetahui Bilangan Ordinal seperti Pertama, Kedua, Ketiga, Keempat dalam Bahasa Indonesia atau juga First (1st), Second (2nd), Third (3rd), Fourth (4th) dalam Bahasa Inggris, atau mungkin dalam Bahasa Asing lainnya seperti beberapa Bahasa di Eropa dan Asia/Chinese (第一, 第二, 第三, 第四).
Kali ini kita akan menjelaskannya lebih dalam tentang Ordinal dan Kardinal dalam Matematika (Teori Himpunan) dan Ilmu Googologi, mulai dari Ordinal Omega sampai dengan Collapsing Function.
PENGERTIAN

Sumber : Wikipedia.org (Ordinal Number), Wikipedia.org (Ordinal Arithmetic), Wikipedia.org (Ordinal Notation), Googology.wikia.org (Ordinal), Johncarlosbaez.Wordpress.com (Ordinals Part 1, Part 2, Part 3)
Dalam Teori Himpunan, Bilangan Ordinal merujuk pada jenis tatanan tertentu dalam suatu himpunan yang diatur dengan baik, biasanya diidentifikasi sebagai Himpunan Transitif Hereditari. Bilangan ordinal merupakan perluasan dari bilangan asli dan berbeda dari integer serta bilangan kardinal. Seperti jenis bilangan lainnya, Bilangan Ordinal mendukung operasi penjumlahan, perkalian, dan pemangkatan.
Georg Cantor memperkenalkan konsep Bilangan Ordinal pada tahun 1883 untuk menangani urutan tak terhingga dan mengklasifikasikan Himpunan Turunan. Ide ini muncul saat dia mempelajari sifat-sifat unik Deret Trigonometri pada tahun 1872.
Setiap Bilangan Ordinal didefinisikan oleh himpunan ordinal yang mendahuluinya. Secara umum, definisi ordinal mengidentifikasi setiap ordinal sebagai himpunan ordinal yang mendahuluinya. Contohnya, Ordinal 42 adalah jenis ordinal yang terdiri dari ordinal dari 0 (ordinal terkecil) hingga 41 (pendahulu langsung dari 42) dan dapat diidentifikasi sebagai Himpunan {0,1,2,…,41}.
Ordinal tak hingga, seperti ω, adalah konsep yang penting. ω merupakan Ordinal Tak Hingga terkecil dan merupakan jenis ordinal dari bilangan asli. ω bahkan dapat diidentifikasi dengan himpunan bilangan asli. Himpunan bilangan asli terurut dengan baik, dan karena tertutup ke bawah, dapat diidentifikasi dengan ordinal yang terkait (sesuai dengan definisi ω).
Intuisi Ordinal yang lebih jelas mungkin dapat dibentuk dengan memeriksa beberapa di antaranya seperti yang disebutkan di atas, mereka mulai dengan bilangan asli, 0, 1, 2, 3, 4, 5, ... Setelah semua bilangan asli datang ordinal tak terbatas pertama, ω, dan setelah itu muncul ω+1, ω+2, ω+3, dan seterusnya. (Persisnya arti penjumlahan akan ditentukan nanti anggap saja mereka sebagai nama.) Setelah semua ini muncul ω·2 (yaitu ω+ω), ω·2+1, ω·2+2, dan seterusnya, lalu ω·3, dan kemudian ω·4. Sekarang himpunan ordinal yang dibentuk dengan cara ini (ω·m+n, di mana m dan n adalah bilangan asli) harus memiliki ordinal yang terkait dengannya: dan itu adalah ω2. Selanjutnya, akan ada ω3, lalu ω4, dan seterusnya, dan ωω ( ), lalu
), lalu  , lalu
, lalu  , dan bahkan kemudian ε0 (
, dan bahkan kemudian ε0 ( ) (Epsilon Nought / Epsilon Nol) (untuk memberikan beberapa contoh ordinal yang relatif kecil—dapat dihitung). Ini dapat dilanjutkan tanpa batas (Karena setiap kali seseorang mengatakan "dan seterusnya" ketika menghitung ordinal, itu mendefinisikan ordinal yang lebih besar). Ordinal tak terhitung terkecil adalah himpunan semua ordinal terhitung, dinyatakan sebagai ω1 atau Ω.
) (Epsilon Nought / Epsilon Nol) (untuk memberikan beberapa contoh ordinal yang relatif kecil—dapat dihitung). Ini dapat dilanjutkan tanpa batas (Karena setiap kali seseorang mengatakan "dan seterusnya" ketika menghitung ordinal, itu mendefinisikan ordinal yang lebih besar). Ordinal tak terhitung terkecil adalah himpunan semua ordinal terhitung, dinyatakan sebagai ω1 atau Ω.
Atau yang lebih sederhananya seperti ini urutannya :
ω, ω + 1, ω + 2, …, ω·2, ω·2 + 1, …, ω2, …, ω3, …, ωω, …, ωωω, …, ε0, …
A. Definisi Utama
Di sini kami akan menjelaskan beberapa cara Formal dan Informal untuk memperkenalkan Sistem Bilangan Ordinal.
Sebagai Perpanjangan/Ekstensi dari Bilangan Asli
Paling mudah untuk berpikir secara intuitif tentang ordinal sebagai perpanjangan dari bilangan bulat non-negatif. Bilangan bulat nonnegatif adalah 0, 1, 2, 3, 4, ..., tetapi sistem ordinal memperluas ini dengan Ordinal Transfinit Pertama ω. Omega (ω) adalah Ordinal Pertama yang lebih besar dari semua bilangan asli.
Selanjutnya kita dapat melanjutkan dengan Ordinal ω+1. Anehnya, definisi penambahan ordinal memberi tahu kita bahwa ini berbeda dari 1+ω, yang sama dengan ω. ω+1, bagaimanapun, lebih besar dari ω. Tentu saja ada ordinal lebih lanjut seperti ω+2, ω+3, dll. dan akhirnya kita mencapai ω+ω.
Banyaknya cara menjumlahkan n Ordinal diberikan oleh Barisan 1, 2, 5, 13, 33, 81, 193, 449, … (OEIS A005348).
ω+ω juga dapat ditulis ω×2. Anehnya, 2×ω=ω (Ini dijelaskan pada bagian di bawah tentang ordinal Transfinit kecil). Kemudian datang ω×3, ω×4, ω×5, dan seterusnya hingga mencapai ω×ω=ω2, diikuti oleh ω3, ω4, ..., ωω, ωω+1, ωωω,  , ...
, ...
Sangat penting untuk tidak lupa bahwa banyak Ordinal Perantara (Intermediate Ordinals), seperti  , masih dihitung di sini, dan tidak ketinggalan.
, masih dihitung di sini, dan tidak ketinggalan.
Jenis Orde
Jenis pesanan adalah cara paling umum untuk mendefinisikan Ordinal. Di bawah definisi ini, Ordinal adalah Kelas Ekivalen dari Himpunan yang tertata baik di bawah relasi Isomorfisme orde.
Relasi Biner ≤ adalah Orde yang baik dari Himpunan S jika semua berikut ini benar untuk semua a, b, c dalam S :
- Setiap himpunan bagian dari S memiliki Elemen Minimum.
Himpunan a yang Tertata baik (Well-ordered Set or Woset) terdiri dari himpunan S dan Relasi ≤S yang merupakan Himpunan S yang terurut dengan baik.
Suatu orde Isomorfisme antara dua Woset (Himpunan yang tertata baik) (S, ≤S) dan (T, ≤T) adalah bijeksi f: S↦T sedemikian sehingga ∀x, y ∈ S: x ≤S y ⇔ f(x) ≤T f(y). Kita katakan bahwa dua ordo adalah isomorfik orde jika terdapat orde isomorfisme di antara keduanya. Tidak sulit untuk menunjukkan bahwa relasi isomorfik orde adalah relasi ekivalensi, dan dengan demikian mempartisi semua himpunan yang terurut dengan baik ke dalam kelas ekivalen, yang akan kita sebut tipe orde. Setiap jenis pesanan diwakili oleh ordinal yang berbeda.
Semua Woset kosong saling orde Isomorfik, dan dua woset dengan kardinalitas berbeda tidak bisa orde isomorfik, sehingga woset kosong membentuk tipe orde. Kami akan memberi label kelas ini "0". Dengan lebih sulit, dapat ditunjukkan bahwa untuk semua kardinal berhingga n, woset dengan kardinalitas n membentuk suatu tipe orde yang kita sebut n. Jadi kita sudah memiliki ordinal 0, 1, 2, 3, ...
Jenis urutan woset dengan elemen terbesar disebut Ordinal Penerus (Successor Ordinal). Ordinal yang bukan ordinal penerus atau 0 disebut Ordinal Limit (Limit Ordinals). Untuk setiap ordinal α, ada ordinal penerus minimal β>α yang kita sebut penerus α, dinotasikan α+1.
B. Definisi dalam Induksi Transfinit (Transfinite Induction)
Induksi Transfinit berlaku di setiap himpunan yang tertata dengan baik, tetapi sangat penting dalam kaitannya dengan ordinal sehingga perlu dinyatakan kembali di sini.
Setiap properti yang berpindah dari himpunan ordinal yang lebih kecil dari ordinal tertentu ke itu sendiri, berlaku untuk semua ordinal.
Artinya, jika P(α) benar setiap kali P(β) benar untuk semua β < α , maka P(α) benar untuk semua α. Atau, lebih praktisnya untuk membuktikan properti P untuk semua ordinal α, dapat diasumsikan bahwa ia sudah diketahui untuk semua β < α yang lebih kecil.
[Untuk membaca lebih lengkapnya tentang Topik ini, silahkan lihat di sini (Transfinite Induction).]
Suksesor (Successor) dan Limit Ordinal
Setiap ordinal bukan nol memiliki elemen minimum, nol. Ini mungkin atau mungkin tidak memiliki elemen maksimum. Misalnya, 42 memiliki maksimum 41 dan ω+6 memiliki maksimum ω+5. Di sisi lain, ω tidak memiliki maksimum karena tidak ada bilangan asli terbesar. Jika suatu ordinal memiliki maksimum α, maka ordinal tersebut adalah ordinal berikutnya setelah α, dan disebut Ordinal Penerus (Successor Ordinal), yaitu Penerus/Suksesor α, ditulis α+1. Dalam definisi Ordinal Von Neumann, Suksesor dari α adalah  karena elemen-elemennya adalah elemen dari α dan α itu sendiri.
karena elemen-elemennya adalah elemen dari α dan α itu sendiri.
Ordinal bukan nol yang bukan Penerus disebut Ordinal Batas (Limit Ordinal). Satu pembenaran untuk istilah ini adalah bahwa Ordinal Batas adalah batas dalam pengertian Topologi dari semua ordinal yang lebih kecil (di bawah Topologi Orde / Order Topology).
Ketika  adalah barisan berindeks ordinal, diindeks oleh limit γ dan urutannya meningkat, yaitu
adalah barisan berindeks ordinal, diindeks oleh limit γ dan urutannya meningkat, yaitu  kapanpun
kapanpun  limitnya didefinisikan sebagai batas atas terkecil dari himpunan
limitnya didefinisikan sebagai batas atas terkecil dari himpunan  yaitu, ordinal terkecil (selalu ada) lebih besar dari suku mana pun dari barisan tersebut. Dalam pengertian ini, limit ordinal adalah limit dari semua ordinal yang lebih kecil (diindeks dengan sendirinya). Secara lebih langsung, itu adalah supremum dari himpunan ordinal yang lebih kecil.
yaitu, ordinal terkecil (selalu ada) lebih besar dari suku mana pun dari barisan tersebut. Dalam pengertian ini, limit ordinal adalah limit dari semua ordinal yang lebih kecil (diindeks dengan sendirinya). Secara lebih langsung, itu adalah supremum dari himpunan ordinal yang lebih kecil.
Cara lain untuk mendefinisikan ordinal limit adalah dengan mengatakan bahwa α adalah ordinal limit jika dan hanya jika :
Ada ordinal yang lebih kecil dari α dan setiap kali ζ adalah ordinal yang lebih kecil dari α, maka ada ordinal ξ sedemikian rupa sehingga ζ < ξ < α.
Jadi dalam urutan berikut :
0, 1, 2, …, ω, ω+1
ω adalah ordinal limit karena untuk sembarang ordinal yang lebih kecil (dalam contoh ini, bilangan asli) ada ordinal lain (bilangan asli) yang lebih besar darinya, tetapi masih lebih kecil dari ω.
Jadi, setiap ordinal adalah nol, atau Penerus/Suksesor (dari Pendahulu/Predesesor yang terdefinisi dengan baik), atau batas. Perbedaan ini penting, karena banyak definisi oleh rekursi transfinite bergantung padanya. Sangat sering, ketika mendefinisikan fungsi F dengan rekursi transfinit pada semua ordinal, satu mendefinisikan F(0), dan F(α+1) dengan asumsi F(α) didefinisikan, dan kemudian, untuk ordinal limit δ satu mendefinisikan F(δ) sebagai limit dari F(β) untuk semua β<δ (baik dalam pengertian limit ordinal, seperti dijelaskan sebelumnya, atau untuk beberapa pengertian limit lainnya jika F tidak mengambil nilai ordinal). Dengan demikian, langkah yang menarik dalam definisi adalah langkah Suksesor, bukan ordinal batas. Fungsi seperti itu (terutama untuk F yang tidak menurun dan mengambil nilai Ordinal) disebut Kontinu. Penjumlahan Ordinal, Perkalian dan Eksponensial Kontinu sebagai Fungsi dari argumen kedua mereka (tetapi dapat didefinisikan secara non-rekursif).
Mengindeks Kelas Ordinal
Setiap himpunan yang terurut dengan baik adalah serupa (orde-isomorfik) dengan bilangan ordinal unik α; dengan kata lain, elemen-elemennya dapat diindeks secara meningkat dengan ordinal kurang dari α. Ini berlaku, khususnya, untuk setiap set ordinal: setiap set ordinal secara alami diindeks oleh ordinal kurang dari beberapa {\displaystyle \alpha }\alpha . Hal yang sama berlaku, dengan sedikit modifikasi, untuk kelas ordinal (kumpulan ordinal, mungkin terlalu besar untuk membentuk himpunan, ditentukan oleh beberapa properti): setiap kelas ordinal dapat diindeks oleh ordinal (dan, ketika kelas tidak dibatasi di kelas semua ordinal, ini menempatkannya di kelas-bijeksi dengan kelas semua ordinal). Jadi elemen γ di kelas (dengan konvensi bahwa "0-th" adalah yang terkecil, "1-st" adalah yang terkecil berikutnya, dan seterusnya) dapat diucapkan dengan bebas dari. Secara formal, definisinya adalah dengan induksi transfinit: elemen γ dari kelas didefinisikan (asalkan telah didefinisikan untuk semua β < γ), sebagai elemen terkecil yang lebih besar dari elemen β untuk semua β < γ.
Ini dapat diterapkan, misalnya, ke kelas ordinal limit : Ordinal γ, yang merupakan limit atau nol adalah ω·γ (Lihat Aritmatika Ordinal untuk definisi perkalian ordinal). Demikian pula, seseorang dapat mempertimbangkan ordinal aditif yang tidak dapat diurai (Artinya ordinal bukan nol yang bukan jumlah dari dua ordinal yang lebih kecil) : γ ordinal yang tidak dapat didekomposisi secara aditif diindeks sebagai  . Teknik pengindeksan kelas ordinal sering berguna dalam konteks titik tetap: misalnya, γ ordinal α sedemikian rupa sehingga
. Teknik pengindeksan kelas ordinal sering berguna dalam konteks titik tetap: misalnya, γ ordinal α sedemikian rupa sehingga  ditulis
ditulis  . Ini disebut "angka Epsilon".
. Ini disebut "angka Epsilon".
[Untuk membaca lebih lengkapnya tentang Topik ini, silahkan lihat di sini Ordinal Number).]
Perbedaan Ordinal dengan Kardinal
Cantor menemukan 2 (Dua) jenis Ketakhingaan yaitu Kardinal dan Ordinal. Kardinal mengatakan seberapa besar himpunannya. Dua Himpunan dapat dimasukkan ke dalam korespondensi 1-1 jika mereka memiliki jumlah elemen yang sama — di mana 'angka' semacam ini adalah kardinal. Anda mungkin pernah mendengar tentang kardinal seperti Alef Nol / Aleph-Nought /  (Jumlah Bilangan Bulat), 2 Pangkat Alef-Nol/Aleph-Nought (
(Jumlah Bilangan Bulat), 2 Pangkat Alef-Nol/Aleph-Nought ( ) (Jumlah Bilangan Real), dan seterusnya. Anda mungkin pernah mendengar desas-desus tentang kardinal yang jauh lebih besar, seperti 'kardinal yang tidak dapat diakses' atau 'kardinal yang sangat besar'. Semua ini sangat menyenangkan, dan saya sarankan mulai dari sini :
) (Jumlah Bilangan Real), dan seterusnya. Anda mungkin pernah mendengar desas-desus tentang kardinal yang jauh lebih besar, seperti 'kardinal yang tidak dapat diakses' atau 'kardinal yang sangat besar'. Semua ini sangat menyenangkan, dan saya sarankan mulai dari sini :
- Frank R. Drake, Set Theory, an Introduction to Large Cardinals, North-Holland, 1974.
Dan sebenarnya ada banyak Sumber-sumber lainnya yang membahas tentang Ordinal dan Kardinal. Ordinal mengatakan seberapa besar set 'Teratur dengan baik (Well-ordered)'. Suatu himpunan terurut dengan baik jika ia datang dengan suatu relasi ≤ mematuhi aturan biasa :
- Transitivitas (Transitivity) : Jika x ≤ y dan y ≤ z maka x ≤ z
- Refleksivitas (Reflexivity) : x ≤ x
- Antisimetri (Antisymmetry) : Jika x ≤ y dan y ≤ x maka x = y
Dan satu aturan lagi yaitu : Setiap subset tak kosong memiliki Elemen terkecil.
Contohnya :
1. Himpunan Kosong :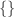
Terurut dengan baik dengan cara yang sepele, dan ordinal yang sesuai disebut sebagai 0.
2. Demikian pula, Himpunan apa pun dengan hanya satu Unsur, seperti ini :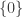
Teratur dengan baik dengan cara yang sepele, dan ordinal yang sesuai disebut sebagai 1.
3. Demikian pula, setiap himpunan dengan Dua Elemen, seperti ini :
Menjadi tertata dengan baik segera setelah kami memutuskan elemen mana yang lebih besar; pilihan yang jelas adalah mengatakan 0 < 1. Ordinal yang sesuai disebut sebagai 2.
4. Demikian pula, setiap himpunan dengan Tiga Elemen, seperti ini :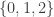
menjadi tertata dengan baik segera setelah kita mengurutkannya secara linier; pilihan yang jelas di sini adalah mengatakan 0 < 1 < 2. Ordinal yang sesuai disebut sebagai 3.
Mungkin Anda mendapatkan polanya — Anda mungkin pernah melihat ordinal khusus ini sebelumnya, mungkin di sekolah dasar. Mereka disebut ordinal hingga, atau "bilangan asli".
Tapi ada trik lucu yang mungkin tidak mereka ajarkan kepada Anda saat itu: kita dapat mendefinisikan setiap ordinal menjadi himpunan semua ordinal yang kurang dari itu :
Dan seterusnya. Ini bagus karena sekarang setiap ordinal adalah kumpulan ukuran yang tertata dengan baik yang merupakan singkatan dari ordinal. Dan, kita dapat mendefinisikan satu ordinal menjadi "kurang dari atau sama" dengan ordinal lain tepat ketika itu adalah subset dari yang lain.
C. Ordinal Aritmetik
Dalam Matematika Teori Himpunan, Aritmatika Ordinal menguraikan tiga operasi dasar pada bilangan ordinal, yaitu Penjumlahan, Perkalian, dan Perpangkatan (serta Tetrasi). Setiap operasi ini dapat didefinisikan secara mendasar melalui dua pendekatan yang berbeda: pembangunan himpunan terurut eksplisit yang merepresentasikan hasil operasi atau melalui penggunaan rekursi transfinite. Bentuk normal Cantor digunakan sebagai cara standar untuk menuliskan ordinal. Selain dari Operasi Ordinal konvensional, ada juga Aritmatika Ordinal "Asli" dan Operasi Gesit (Nimber Operations).
1. Penjumlahan (Addition)
Namun, penambahan masih bersifat asosiatif; orang dapat melihat misalnya bahwa (ω+4)+ω = ω+(4+ω) = ω+ω.
Definisi penambahan juga dapat diberikan secara Induktif (Induksi berikut pada) :
- α+0 = α,
- α+(β+1) = (α+β)+1 (Di sini, "+1" menunjukkan Suksesor sebuah Ordinal),
- Dan jika β adalah ordinal limit maka α+β adalah limit dari α+δ untuk semua δ<β.
Dengan menggunakan definisi ini, ω+3 dapat dilihat sebagai suatu ordinal penerus (merupakan penerus dari ω+2), sedangkan 3+ω adalah suatu ordinal limit, yaitu limit dari 3+0 = 3, 3+1 = 4, 3+2 = 5, dst., yang hanya ω.
Nol adalah Identitas Aditif α+0 = 0+α = α. Penjumlahan bersifat Asosiatif (α+β)+γ = α+(β+γ).
Penambahan secara ketat meningkat dan terus menerus dalam argumen yang benar :
Tetapi hubungan analogi tidak berlaku untuk argumen kiri; sebagai gantinya kami hanya memiliki :
Penjumlahan ordinal adalah Kanselatif Kiri (Left-Cancellative) : jika α+β = α+γ, maka β = γ. Selanjutnya, seseorang dapat mendefinisikan pengurangan kiri untuk ordinal β ≤ α : ada γ unik sehingga α = β+γ. Di sisi lain, pembatalan hak tidak berfungsi :
tapi
Pengurangan benar juga tidak, bahkan ketika β ≤ α : misalnya, tidak ada γ sehingga γ+42 = ω.
Jika ordinal yang kurang dari ditutup dengan penjumlahan dan mengandung 0 maka α kadang-kadang disebut bilangan γ (lihat ordinal aditif yang tidak dapat didekomposisi). Ini persis ordinal dari bentuk ωβ.
Contohnya adalah :
Apa yang datang setelah semua ordinal yang terbatas? Nah, himpunan semua ordinal berhingga itu sendiri terurut dengan baik :
Jadi, ada ordinal yang sesuai dengan ini — dan ini adalah ordinal tak terbatas pertama. Biasanya disebut ω, diucapkan 'omega'. Menggunakan trik lucu yang saya sebutkan, kita benar-benar dapat mendefinisikan
Apa yang datang setelah ini? Nah, ternyata ada satu set yang tertata dengan baik
berisi ordinal hingga bersama dengan \omega, dengan gagasan yang jelas tentang "kurang dari" ω lebih besar dari yang lain. Sesuai dengan set ini ada ordinal yang disebut
Seperti biasa, kita cukup mendefinisikan
Pada titik ini Anda mungkin akan bingung jika Anda tahu tentang kardinal, jadi izinkan saya untuk meyakinkan. Himpunan ω dan ω+1 memiliki kardinalitas yang sama: keduanya dapat dihitung. Dengan kata lain, Anda dapat menemukan fungsi 1-1 dan ke antara set ini. Tetapi ω dan ω+1 berbeda sebagai ordinal, karena Anda tidak dapat menemukan fungsi 1-1 dan ke di antara keduanya yang mempertahankan urutan. Ini mudah dilihat, karena ω+1 memiliki elemen terbesar sedangkan ω tidak.
Memang, semua ordinal dalam rangkaian posting ini akan dapat dihitung! Jadi untuk yang tak terbatas, Anda dapat membayangkan bahwa semua yang saya lakukan adalah mengambil set favorit Anda yang dapat dihitung dan memesannya dengan cara yang lebih licik.
Oke, jadi kita sampai pada ω+1. Apa yang terjadi selanjutnya? Yah, tidak mengherankan, itu
Kemudian datang
dan seterusnya. Anda mendapatkan idenya.
Kejutan utama adalah bahwa penambahan ordinal tidak komutatif. Kami telah melihat bahwa  , sejak
, sejak
adalah daftar hal yang tak terbatas ... dan kemudian satu hal lagi yang datang setelah semua itu!. Tetapi 1+ω = ω, karena satu hal yang diikuti oleh daftar tak terhingga banyak lagi hanyalah daftar tak terhingga banyak hal.
Dengan ordinal, ini bukan hanya tentang kuantitas, tetapi urutannya penting!
2. Perkalian (Multiplication)
Distribusi sebagian berlaku untuk aritmatika ordinal: α(β+γ) = αβ+αγ. Namun, hukum distributif lainnya (β+γ)α = βα+γα umumnya tidak benar : (1+1)·ω = 2·ω = ω sedangkan 1·ω+1·ω = ω+ω, yang berbeda . Oleh karena itu, bilangan urut membentuk hampir semiring kiri, tetapi tidak membentuk cincin.
Definisi perkalian juga dapat diberikan secara induktif (induksi berikut pada) :
- α·0 = 0,
- α·(β+1) = (α·β)+α,
- Dan jika β adalah ordinal limit maka α·β adalah limit dari α·δ untuk δ < β.
Sifat utama Perkalian adalah :
- α·0 = 0·α = 0.
- Satu (1) adalah identitas perkalian α·1 = 1·α = α.
- Perkalian bersifat asosiatif (α·β)·γ = α·(β·γ).
- Perkalian meningkat secara ketat dan berkelanjutan dalam argumen yang benar: (α < dan > 0) ⇒ γ·α < γ·β
- Perkalian tidak benar-benar meningkat dalam argumen kiri, misalnya, 1 < 2 tetapi 1·ω = 2·ω = ω = . Namun, ini (tidak ketat) meningkat, yaitu α ≤ β ⇒ α·γ ≤ β·γ.
- Ada Hukum Pembatalan Kiri : Jika α > 0 dan α·β = α·γ, maka β = γ.
- Pembatalan hak tidak berfungsi, mis. 1·ω = 2·ω = ω, tetapi 1 dan 2 berbeda.
- α·β = 0 ⇒ α = 0 atau β = 0.
- Hukum Distributif di sebelah Kiri : α·(β+γ) = α·β+α·γ
- Tidak ada hukum distributif di sebelah kanan. mis. (ω+1)·2 = ω+1+ω+1 = ω+ω+1 = ω·2+1, yang bukan ω·2+2.
- Pembagian kiri dengan sisa untuk semua α dan β, jika β > 0, maka ada γ dan δ yang unik sehingga α = β·γ+δ and δ < β. (Namun ini tidak berarti ordinal adalah domain Euclidean, karena mereka bahkan bukan ring, dan "norma" Euclidean bernilai ordinal.)
- Pembagian kanan tidak bekerja: tidak ada sehingga α·ω ≤ ωω ≤ (α+1)·ω.
Sebuah Bilangan δ (Lihat Perkalian yang Tidak dapat didekomposisi / Multiplicatively Indecomposable) adalah lebih besar ordinal dari 1 sehingga αβ = β setiap kali 0<α<β. Ini terdiri dari ordinal 2 dan ordinal dari bentuk ωωβ.
Contohnya adalah :
Oke, jadi kita telah melihat Ordinal ini :
Apa selanjutnya?
Nah, urutan setelah semua ini disebut ω+ω. Orang sering menyebutnya “omega kali 2” atau disingkat ω2. Begitu,
Akan menyenangkan memiliki buku dengan halaman ω, setiap halaman setebal setengah halaman sebelumnya. Anda dapat menceritakan kisah panjang yang menyenangkan dengan buku berukuran ω. Saya pikir Anda bisa membayangkan ini. Dan jika Anda meletakkan satu buku seperti itu di sebelah yang lain, itu adalah gambaran yang bagus dari \omega 2.
Perlu dicatat bahwa ω2 tidak sama dengan 2ω. Kita punya
sementara
di mana kita menambahkan \omega dari istilah-istilah ini. Tapi
begitu
Dengan menggunakan ini, Anda dapat membuktikan bahwa apa yang saya katakan adalah benar. Meskipun demikian, saya harap Anda melihat mengapa apa yang saya katakan mungkin masuk akal. Seperti penjumlahan ordinal, perkalian ordinal tidak komutatif! Jika Anda tidak menyukai ini, Anda harus mempelajari kardinal sebagai gantinya.
Apa selanjutnya? Nah, kemudian datang
dan seterusnya. Tapi Anda mungkin sudah memahami ini, jadi kita bisa langsung melompat ke ω3.
Bahkan, Anda mungkin siap untuk langsung beralih ke ω4, dan ω5, dan seterusnya.
3. Perpangkatan/Eksponensial (Exponentiation)
Secara umum, setiap ordinal α dapat dipangkatkan ke ordinal lain β dengan cara yang sama untuk mendapatkan αβ.
Hal ini paling mudah untuk dijelaskan dengan menggunakan definisi ordinal Von Neumann sebagai himpunan semua ordinal yang lebih kecil. Kemudian, untuk membangun satu set bertipe orde αβ pertimbangkan semua fungsi dari β hingga α sedemikian rupa sehingga hanya sejumlah elemen dari domain β yang dipetakan ke elemen bukan nol dari (pada dasarnya, kami mempertimbangkan fungsi dengan dukungan hingga). Urutannya adalah Leksikografis (Lexicographic) dengan posisi paling tidak signifikan terlebih dahulu. Dan kita menemukan :
- 1ω = 1,
- 2ω = ω,
- 2ω+1 = ω·2 = ω+ω.
Definisi Eksponen juga dapat diberikan secara Induktif (Induksi berikut adalah pada β, Eksponen) :
- α0 = 1,
- αβ+1 = (αβ)·α, dan
- Jika β adalah Limit Ordinal, maka αβ adalah Limit dari αδ untuk semua δ < β.
Sifat-sifat Eksponen Ordinal :
- α0 = 1.
- Jika 0 < α, maka 0α = 0.
- 1α = 1.
- α1 = α.
- αβ·αγ = αβ + γ.
- (αβ)γ = αβ·γ.
- Ada α, β, dan γ yang (α·β)γ ≠ αγ·βγ. Misalnya, (ω·2)2 = ω·2·ω·2 = ω2·2 ≠ ω2·4.
- Eksponen Ordinal meningkat secara ketat dan terus menerus dalam Argumen Kanan : Jika γ > 1 dan α < β, maka γα < γβ.
- Jika α < β, maka αγ ≤ βγ. Perhatikan, misalnya, bahwa 2 < 3 namun 2ω = 3ω = ω.
- Jika α > 1 dan αβ = αγ, maka β = γ. Jika α = 1 atau α = 0 tidak demikian.
- Untuk semua α dan β, jika β > 1 dan α > 0 maka terdapat yang unik sedemikian γ, δ, dan ρ sehingga α = βγ·δ + ρ sehingga 0 < δ < β dan ρ < βγ.
Sementara Notasi yang sama digunakan untuk Eksponensial Ordinal dan Eksponensial Kardinal, Eksponensial Ordinal sangat berbeda dari Eksponensial Kardinal. Misalnya, dengan Eksponensial Ordinal  , tetapi untuk
, tetapi untuk  (Aleph Naught / Alef Nol, Kardinalitas dari ω),
(Aleph Naught / Alef Nol, Kardinalitas dari ω),  . Di sini,
. Di sini,  adalah kardinalitas himpunan semua fungsi dari himpunan semua bilangan asli ke himpunan dengan dua elemen. (Ini adalah Kardinalitas dari himpunan pangkat dari himpunan semua bilangan asli dan sama dengan
adalah kardinalitas himpunan semua fungsi dari himpunan semua bilangan asli ke himpunan dengan dua elemen. (Ini adalah Kardinalitas dari himpunan pangkat dari himpunan semua bilangan asli dan sama dengan  , Kardinalitas Kontinum.) Untuk menghindari ordinalitas yang membingungkan eksponensial dengan eksponensial kardinal, seseorang dapat menggunakan simbol untuk ordinal (misalnya ω) di yang pertama dan simbol untuk kardinal (Misalnya
, Kardinalitas Kontinum.) Untuk menghindari ordinalitas yang membingungkan eksponensial dengan eksponensial kardinal, seseorang dapat menggunakan simbol untuk ordinal (misalnya ω) di yang pertama dan simbol untuk kardinal (Misalnya  ) di yang terakhir.
) di yang terakhir.
Jacobsthal menunjukkan bahwa satu-satunya solusi dari αβ = βα dengan α ≤ β diberikan oleh α = β , atau α = 2 dan β = 4, atau adalah sembarang limit ordinal dan β = εα di mana ε adalah bilangan yang lebih besar dari α.
Contohnya adalah :
Faktanya, saya yakin sekarang Anda siap untuk melompat ke "omega kali omega", atau singkatnya ω2 :
Misalkan Anda memiliki ensiklopedia dengan ω volume, masing-masing menjadi buku dengan ω halaman. Jika setiap buku dua kali lebih tipis dari sebelumnya, Anda akan memiliki ω2 halaman — dan itu masih bisa muat di satu rak buku! Inilah idenya :

Apa yang terjadi selanjutnya? Yah, kita punya
dan seterusnya, dan setelah semua ini datang
dan seterusnya — dan akhirnya
dan kemudian banyak lagi, dan kemudian
ω2·3
dan kemudian banyak lagi, dan kemudian
ω2·4
dan kemudian banyak lagi, dan lebih banyak lagi, dan akhirnya
ω2·ω = ω3
Anda mungkin dapat membayangkan sebuah rak buku berisi ω ensiklopedia, masing-masing dengan ω volume, masing-masing dengan ω halaman, dengan total ω3 halaman. Itu ω3.
Saya telah melewatkan lebih banyak langkah agar Anda tidak bosan. Saya tahu Anda memiliki banyak hal yang harus dilakukan dan tidak dapat menghabiskan banyak waktu untuk membaca ini, bahkan jika subjeknya tak terhingga.
Jadi jika Anda tidak keberatan saya hanya menyebutkan beberapa poin tinggi, ada orang-orang seperti ω4 dan ω5 dan seterusnya, dan setelah semua ini datang
ωω
Coba kita bayangkan ini! Pertama, bayangkan sebuah buku dengan halaman ω. Kemudian bayangkan Ensiklopedia Buku seperti ini, dengan ω volume. Lalu bayangkan sebuah rak buku berisi ω ensiklopedia seperti ini. Lalu bayangkan sebuah ruangan yang berisi ω rak buku seperti ini. Kemudian bayangkan sebuah lantai dengan perpustakaan dengan ω kamar seperti ini. Lalu bayangkan perpustakaan dengan ω lantai seperti ini. Kemudian bayangkan sebuah kota dengan perpustakaan ω seperti ini. Dan seterusnya, Tak Terhingga (Infinitum).
Anda harus sedikit berhati-hati di sini, atau Anda akan membayangkan jumlah halaman yang tak terhitung jumlahnya. Untuk memberi nama halaman tertentu di alam semesta ini, Anda harus mengatakan sesuatu seperti ini :
Halaman ke-23 dari Buku ke-107 dari Ensiklopedia ke-20 di Rak Buku ke-7 di Ruang 0 di Lantai 1000 Perpustakaan ke-973 di Kota ke-6 di Benua ke-0 di Planet ke-0 di Tata Surya ke-0 di…
Seperti yang mereka katakan,
Tetapi untuk Eksponen Tak Terbatas (Infinite Exponents), definisinya mungkin Tidak Jelas (Obvious).
Berikut adalah gambar ωω, diambil dari halaman web interaktif David Madore yang luar biasa :
Di halamannya, jika Anda mengklik salah satu label untuk bagian awal dari sebuah ordinal, seperti ω, ω2, ω3 atau ω4 di sini, gambar akan meluas untuk menunjukkan bagian itu!
Dan inilah gambar lain, di mana setiap putaran jarum jam membawa Anda ke kekuatan \omega yang lebih tinggi :
 |
| KETERANGAN : Gambar ini juga ada di atas. |
4. Bentuk Normal Cantor (Cantor Normal Form)
Setiap bilangan urut α dapat ditulis secara unik sebagai  , di mana k adalah Bilangan Asli, c1, c2, …, ck adalah Bilangan Bulat Positif, dan
, di mana k adalah Bilangan Asli, c1, c2, …, ck adalah Bilangan Bulat Positif, dan  adalah bilangan urut. Penguraian ini disebut bentuk normal Cantor dari , dan dapat dianggap sebagai sistem bilangan posisi basis ω. Eksponen tertinggi disebut derajat α, dan memenuhi
adalah bilangan urut. Penguraian ini disebut bentuk normal Cantor dari , dan dapat dianggap sebagai sistem bilangan posisi basis ω. Eksponen tertinggi disebut derajat α, dan memenuhi  . Persamaan
. Persamaan  berlaku jika dan hanya jika
berlaku jika dan hanya jika  . Dalam hal ini bentuk normal Cantor tidak menyatakan ordinal dalam bentuk yang lebih kecil; ini bisa terjadi seperti yang dijelaskan di bawah ini.
. Dalam hal ini bentuk normal Cantor tidak menyatakan ordinal dalam bentuk yang lebih kecil; ini bisa terjadi seperti yang dijelaskan di bawah ini.
Variasi kecil dari bentuk normal Cantor, yang biasanya sedikit lebih mudah untuk dikerjakan, adalah mengatur semua angka ci sama dengan 1 dan membiarkan eksponennya sama. Dengan kata lain, setiap bilangan urut dapat ditulis secara unik sebagai  , di mana k adalah bilangan asli , dan
, di mana k adalah bilangan asli , dan  adalah bilangan urut.
adalah bilangan urut.
Variasi lain dari bentuk normal Cantor adalah "perluasan basis δ", di mana diganti dengan sembarang ordinal δ>1, dan bilangan ci adalah ordinal positif yang kurang dari δ.
Bentuk normal Cantor memungkinkan kita untuk secara unik mengekspresikan—dan mengurutkan—ordinal α yang dibangun dari bilangan asli oleh sejumlah operasi aritmatika Penjumlahan, Perkalian dan Eksponensial basis ω : dengan kata lain, dengan asumsi  dalam bentuk normal Cantor, kita juga dapat menyatakan Eksponen dalam bentuk normal Cantor, dan membuat asumsi yang sama untuk seperti untuk dan seterusnya secara rekursif, kita mendapatkan sistem notasi untuk ordinal ini. Misalnya :
dalam bentuk normal Cantor, kita juga dapat menyatakan Eksponen dalam bentuk normal Cantor, dan membuat asumsi yang sama untuk seperti untuk dan seterusnya secara rekursif, kita mendapatkan sistem notasi untuk ordinal ini. Misalnya :
(Menunjukkan Ordinal)
Ordinal ε0 (Epsilon Nol) adalah himpunan nilai ordinal α dari ekspresi aritmatika panjang-hingga dari bentuk normal Cantor yang diturunkan non-trivial di mana non-trivial berarti 1<α ketika 0<α. Ini adalah ordinal terkecil yang tidak memiliki ekspresi aritmatika berhingga dalam suku ω, dan ordinal terkecil sehingga  , yaitu dalam bentuk normal Cantor eksponennya tidak lebih kecil dari ordinal itu sendiri. Ini adalah batas urutan :
, yaitu dalam bentuk normal Cantor eksponennya tidak lebih kecil dari ordinal itu sendiri. Ini adalah batas urutan :
Ordinal ε0 penting untuk berbagai alasan dalam aritmatika (pada dasarnya karena ia mengukur kekuatan teori-bukti dari aritmatika Peano orde pertama yaitu, aksioma Peano dapat menunjukkan induksi transfinit hingga ordinal apa pun yang kurang dari ε0 tetapi tidak hingga ε0 itu sendiri).
Bentuk normal Cantor juga memungkinkan kita untuk menghitung jumlah dan hasil kali ordinal untuk menghitung jumlah, misalnya, kita hanya perlu mengetahui (lihat properti yang tercantum dalam Penjumlahan dan Perkalian) bahwa
if  (if
(if  seseorang dapat menerapkan hukum distributif di sebelah kiri dan menulis ulang ini sebagai
seseorang dapat menerapkan hukum distributif di sebelah kiri dan menulis ulang ini sebagai ) , dan jika
, dan jika  ekspresinya adalah sudah dalam bentuk normal Cantor); dan untuk menghitung produk, fakta penting adalah bahwa ketika dalam bentuk normal Cantor dan
ekspresinya adalah sudah dalam bentuk normal Cantor); dan untuk menghitung produk, fakta penting adalah bahwa ketika dalam bentuk normal Cantor dan  , lalu
, lalu
dan
jika n adalah Bilangan Asli bukan nol.
Untuk membandingkan dua ordinal yang ditulis dalam bentuk normal Cantor, pertama-tama bandingkan , lalu , lalu , lalu , dst. Pada perbedaan pertama, ordinal yang memiliki komponen lebih besar adalah ordinal yang lebih besar. Jika mereka sama sampai yang satu berakhir sebelum yang lain, maka yang berakhir lebih dulu lebih kecil.
Contohnya adalah (Ordinal hingga ε0) :
Oke, jadi kita telah mencapai ωω. Sekarang apa?
Nah, kemudian muncul 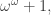 dan seterusnya, tapi saya yakin itu membosankan sekarang. Dan kemudian datang ordinal seperti :
dan seterusnya, tapi saya yakin itu membosankan sekarang. Dan kemudian datang ordinal seperti :
mengarah ke :
Kemudian akhirnya datang ordinal seperti :
dan seterusnya, mengarah ke :
Ini sebenarnya mengingatkan saya pada sesuatu yang terjadi saat berkendara melintasi South Dakota pada suatu musim panas dengan seorang teman saya. Kami masih kuliah, jadi kami libur musim panas, jadi kami berkendara melintasi negara. Kami berkendara melintasi South Dakota dari perbatasan Timur ke Barat di Interstate 90.
Negara bagian ini sangat luas — sekitar 600 Kilometer, dan sebagian besar benar-benar datar, jadi perjalanannya sangat membosankan. Kami terus melihat tanda-tanda untuk sekelompok tempat wisata di tepi barat negara bagian, seperti Tanah tandus dan Mt. Rushmore — gunung yang mereka ukir agar terlihat seperti wajah presiden, hanya untuk memberi orang alasan untuk tetap mengemudi.
Bagaimanapun, saya akan menceritakan sisa ceritanya nanti — saya melihat beberapa ordinal lainnya muncul :
Kami benar-benar melaju sekarang hanya agar tidak bosan — seperti yang saya dan teman saya lakukan di South Dakota. Anda mungkin senang membayangkan bahwa kami memiliki cerita dan lelucon perdagangan yang menyenangkan, seperti yang mereka lakukan di film-film jalanan. Tapi kami berkendara jauh-jauh dari Princeton ke kabin teman saya Chip di California. Saat kami tiba di South Dakota, kami semua kehabisan cerita dan lelucon.
Hei lihat! Nya
Itu keren. Kemudian datang
dan seterusnya.
Anyway, kembali ke cerita saya. Untuk paruh pertama dari setengah perjalanan kami melintasi negara bagian, kami terus melihat tanda-tanda untuk sesuatu yang disebut Museum Traktor Dakota Selatan.
Oh, tunggu, ini ordinal yang menarik :
Mari kita berhenti dan melihat :
Itu keren. Oke, mari kita terus mengemudi. Ini dia :
lalu
lalu
dan akhirnya
dan akhirnya
lalu
dan akhirnya
Setelah beberapa saat kami mencapai
lalu
lalu
lalu
lalu
lalu
dan akhirnya
Ini cukup membosankan, kita sudah melaju sangat cepat, tapi kita masih baru saja menambah kecepatan, dan itu akan memakan waktu cukup lama sebelum kita mencapai sesuatu yang menarik.
Kami bergerak sangat cepat sekarang :
Apa yang datang setelah semua ini?
Pada titik ini kita perlu berhenti untuk gas. Notasi kami untuk ordinal baru saja habis!
Ordinal tidak berhenti; hanya notasi kami yang gagal. Himpunan semua ordinal yang terdaftar hingga sekarang — termasuk semua ordinal yang telah kita lewati — adalah himpunan yang tertata rapi yang disebut
ε0
atau "epsilon-nought". Ini memiliki properti luar biasa yang
Dan ini adalah ordinal terkecil dengan properti ini! Ini terlihat seperti ini :
Ini adalah fakta yang menakjubkan bahwa setiap ordinal yang dapat dihitung adalah Isomorfik, sebagai himpunan yang tertata dengan baik, untuk beberapa subset dari garis nyata. David Madore memanfaatkan ini untuk membuat fotonya.
Dan jika ingin melihat dan mengetahui Limit Ordinal sampai 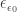 , silahkan lihat pada gambar di bawah ini :
, silahkan lihat pada gambar di bawah ini :
CONTOH URUTAN FUNDAMENTAL (EXAMPLES OF FUNDAMENTAL SEQUENCES)
Sumber : Googology.wikia.org (Fundamental Sequence) [Lalu diterjemahkan melalui Google Translate]
Dalam Googologi yang dapat dihitung (Computable Googology), kita tidak dapat langsung menggunakan ordinal karena mesin Turing tidak menerima Ordinal Transfinit sebagai input. Sebagai gantinya, kami mempertimbangkan analog dari Barisan Fundamental untuk Suku-suku dalam Notasi Rekursif (Recursive Notations), yang disebut aturan ekspansi atau juga barisan fundamental secara luas dalam Googologi. Misalnya, notasi ordinal yang terkait dengan fungsi Buchholz dilengkapi dengan tiga sistem barisan dasar yang berbeda. Arti dari barisan dasar untuk suatu suku dalam notasi ordinal adalah sama dengan ordinal, kecuali untuk penggunaan pengurutan baik rekursif yang diberikan sebagai ganti . Di sisi lain, arti dari barisan dasar untuk suatu istilah dalam notasi umum cukup ambigu.
Urutan Dasar untuk Batas Ordinal λ ≤ ε0 :
Barisan dasar untuk Fungsi Γ :
Urutan dasar untuk Fungsi Theta Feferman (Feferman's Theta Function) :
Atau untuk lebih jelasnya tentang Fungsi Theta Feferman (Feferman's Theta Function), silahkan lihat di bawah ini :
Catatan : Catatan : Fungsi Theta ditampilkan dalam Versi Dua Argumen &space;=&space;\theta_{\alpha}(\beta)) , jika β = 0 dapat disingkat
, jika β = 0 dapat disingkat &space;=&space;\theta(\alpha,&space;0)) , Fungsi Theta adalah perpanjangan dari fungsi Veblen Dua Argumen, untuk Argumen terhitung fungsi theta sama dengan Fungsi Veblen
, Fungsi Theta adalah perpanjangan dari fungsi Veblen Dua Argumen, untuk Argumen terhitung fungsi theta sama dengan Fungsi Veblen &space;=&space;\varphi(\alpha,&space;\beta)) dan memiliki barisan fundamental yang sama, Ω adalah Ordinal Tak Terhitung (Uncountable Ordinal) dan
dan memiliki barisan fundamental yang sama, Ω adalah Ordinal Tak Terhitung (Uncountable Ordinal) dan &space;=&space;\varphi(1,&space;0,&space;0)&space;=&space;\Gamma_{0}) .
.
Barisan Fundamental dapat didefinisikan bahkan untuk ordinal yang tak terhitung jika mereka memiliki Kofinalitas ω. Contoh FS yang valid adalah :
Dan jika ingin melihat Rumus lengkapnya terkait dengan Fungsi Theta Feferman (Feferman's Theta Function), silahkan lihat di bawah ini :
JENIS-JENIS NOTASI ORDINAL FUNDAMENTAL
Sumber : Googology.wikia.org (List of Systems of Fundamental Sequences), Googology.wikia.org (The Extension of Buchholz's Function), dan Googology.wikia.org (My system of number names (Fast Growing Series, FGS)) [Lalu diterjemahkan melalui Google Translate]
Dalam definisi Hierarki (Fast-growing, Hardy, and Slow-growing Hierarchies), hanya ordinal yang dapat dihitung yang digunakan (yaitu ordinal yang lebih kecil dari ordinal pertama yang tidak dapat dihitung ω1). Jika adalah Ordinal Limit yang dapat dihitung maka kofinalitas α selalu sama dengan ω.
Barisan Fundamental untuk bilangan urut batas dengan kofinalitas cof(α) = ω adalah barisan naik ketat (α[n])n<ω dengan panjang dan dengan supremum α, di mana α[n] adalah elemen ke-n dari urutan ini.
A. Wainer Hierarchy (≤ ε0)
Hirarki Wainer adalah metode standar untuk merepresentasikan barisan fundamental untuk ordinal yang kurang dari atau sama dengan ε0.
1. Definisi
Menggunakan Predikat =NF untuk bentuk normal Cantor, kita mendefinisikan sebuah sistem
1. Jika α=NF0, maka [n]:=0. (Dalam hal ini, kami memiliki cof(α)=0.)
- Jika n = 0, maka [n] := 0.
- Jika n ≠ 0, maka [n] := ωα[n[0]].
Jika kurang jelas, silahkan lihat di sini :
Kesalahpahaman Umum
Karena Hierarki Wainer adalah salah satu sistem barisan fundamental yang paling sederhana, para pemula cenderung mempelajari hierarki pada percobaan pertama mereka untuk memahami barisan fundamental. Kemudian mereka cenderung mengacaukan ordinal dan ekspresinya, dan karenanya membuat kesalahan berdasarkan kesalahpahaman ini.
Salah satu kesalahpahaman yang khas adalah mendefinisikan [] dengan spesialisasi parsial, seperti :
Yang mencakup kesalahan/error besar (dalam kasus tertentu, tetapi yang lebih penting tidak semua kasus akurat). Karena variabel tidak dikuantifikasi dengan tepat dengan klarifikasi yang tepat dari rentang yang dilaluinya, domain peta [] tidak terdefinisi dengan baik, dan karenanya [] sendiri tidak terdefinisi. Bahkan jika kita mendefinisikan domain, definisi tersebut tidak bekerja ketika cof(βk) = 1. Bahkan jika kita menerapkan klasifikasi kasus sehingga aturan hanya berlaku untuk kasus cof(βk) = ω, spesialisasi parsial tidak bekerja karena ekspresi ordinal tidak unik. Misalnya, kita memiliki ω2+ωω=ωω, tetapi hasil aturannya tidak unik, seperti yang kita miliki
Masalah ini dengan jelas menjelaskan mengapa kita membutuhkan predikat =NF dalam definisi [].
B. Veblen Hierarchy (≤ Γ0)
1. Definisi
Hirarki Fungsi Veblen (Veblen Function Hierarchy) didefinisikan sebagai berikut :
2. Veblen Normal Form (Bentuk Normal Veblen)
Kami secara bersamaan mendefinisikan :
- Predikat =VNF (Bentuk Normal Veblen);
- Set TV yaitu himpunan ordinal yang dapat dihitung sedemikian rupa sehingga setiap elemen himpunan dapat dilambangkan secara unik hanya dengan menggunakan simbol 0,+,φ di mana menunjukkan hierarki fungsi Unier Veblen;
- Set PV (subset TV yang hanya menyertakan nomor pokok tambahan).
3. Urutan Dasar (Fundamental Sequences)
Barisan dasar untuk limit ordinal α ∈ TV :
C. Fungsi Veblen dari sejumlah argumen yang terbatas (Fungsi Veblen terbatas)
1. Definsi
Misalkan z adalah string kosong atau string yang terdiri dari satu atau lebih nol yang dipisahkan koma 0,0,...,0 dan s adalah string kosong atau string yang terdiri dari satu atau lebih ordinal yang dipisahkan koma α1, α2, ..., αn dengan 1 > 0. Fungsi biner φ(β, γ) dapat ditulis sebagai φ(s, β, z, γ) di mana s dan z adalah string kosong. Fungsi Veblen terhingga didefinisikan sebagai berikut :
2. Bentuk Normal untuk Fungsi Veblen terhingga
Kami secara bersamaan mendefinisikan :
- Predikat FNF (bentuk normal untuk fungsi Veblen Finit);
- Himpunan TF yaitu himpunan ordinal yang dapat dihitung sedemikian rupa sehingga setiap elemen himpunan dapat dilambangkan secara unik hanya dengan menggunakan simbol 0,+,φ di mana menunjukkan fungsi Veblen berhingga;
- Himpunan PF (subset dari TF yang hanya mencakup bilangan pokok aditif).
3. Urutan Dasar (Fundamental Sequences)
Barisan dasar untuk limit ordinal α ∈ TF didefinisikan sebagai berikut :
D. Sistem Urutan Dasar Deedlit (Deedlit’s system of Fundamental Sequences)
2. Bentuk normal untuk Fungsi ϑ
Kami secara bersamaan mendefinisikan :
- Predikat DNF;
- Himpunan TD yaitu himpunan ordinal yang dapat dihitung sedemikian rupa sehingga setiap elemen himpunan dapat dilambangkan secara unik hanya dengan menggunakan simbol 0,+,Ω,ϑ,φ di mana menunjukkan fungsi Veblen biner dan menunjukkan hierarki fungsi runtuh yang didefinisikan dalam subbagian sebelumnya ;
- Himpunan PD (Subset dari TD yang hanya mencakup bilangan pokok tambahan).
Urutan dasar untuk ordinal bukan nol α ∈ TD didefinisikan oleh Deedlit sebagai berikut :
E. Hirarki Buchholz dan Ekstensinya
Untuk penetapan Barisan Fundamental untuk Hierarki ini, kita harus mengizinkan barisan fundamental dengan panjang lebih besar dari dan untuk mendefinisikannya sebagai berikut :
Barisan dasar untuk bilangan urut dengan kofinalitas cof(α) = β adalah barisan naik ketat (α[η])η<β dengan panjang β dan dengan limit α, di mana α[η] adalah elemen ke-η dari urutan ini.
1. Bentuk Normal Buchholz
Kami secara bersamaan mendefinisikan :
- Predikat BNF (Bentuk Normal Buchholz);
- Himpunan TB yaitu himpunan ordinal yang dapat dihitung sehingga setiap elemen himpunan dapat dilambangkan secara unik hanya dengan menggunakan simbol 0,+,ψ di mana menunjukkan hierarki fungsi Buchholz yang diperluas;
- Himpunan PB (Subset dari TB yang hanya mencakup bilangan pokok tambahan).
3. Urutan Dasar (Fundamental Sequences)
Urutan dasar untuk ordinal bukan nol α ∈ TB didefinisikan sebagai berikut :
F. Urutan dasar untuk Fungsi yang Runtuh Kardinal yang Tidak Dapat Diakses dengan Lemah (Fundamental Sequences for the Functions Collapsing Weakly Inaccessible Cardinals)
1. Definisi
Di bagian ini variabel ρ, π dicadangkan untuk kardinal reguler yang tak terhitung jumlahnya dari bentuk  atau
atau  .
.
Kemudian,
Sifat-sifat :
2. Bentuk Normal untuk Fungsi Runtuh Kardinal yang tidak dapat diakses dengan Lemah
Kami secara bersamaan mendefinisikan :
- Predikat WNF;
- Himpunan TW yaitu himpunan ordinal yang dapat dihitung sehingga setiap elemen himpunan dapat dilambangkan secara unik hanya dengan menggunakan simbol 0+, I, Ω, ψ di mana ψ menunjukkan hierarki fungsi runtuh kardinal yang tidak dapat diakses dengan lemah;
- Himpunan PW (Subset dari TW yang hanya mencakup bilangan pokok tambahan).
Barisan dasar untuk bilangan urut α dengan kofinalitas cof(α) = β adalah barisan (α[η])η<β yang meningkat secara ketat dengan panjang β dan dengan limit α, di mana α[η] adalah elemen ke-η dari urutan ini.
Biarkan &space;=&space;1&space;\right&space;\}) menunjukkan Himpunan Ordinal Penerus (Set of Successor Ordinals),
menunjukkan Himpunan Ordinal Penerus (Set of Successor Ordinals), &space;\geq&space;\omega&space;\right&space;\}) menunjukkan himpunan ordinal limit.
menunjukkan himpunan ordinal limit.
Urutan dasar untuk ordinal bukan nol α ∈ TW didefinisikan sebagai berikut :
G. Urutan dasar untuk Fungsi yang Runtuh α-Kardinal yang Tidak Dapat Diakses dengan Lemah (Fundamental sequences for the Functions Collapsing α-Weakly Inaccessible Cardinals)
1. Definisi
Ordinal α-lemah adalah tidak dapat diakses jika itu adalah kardinal biasa yang tak terhitung dan itu adalah batas γ-lemah kardinal yang tidak dapat diakses untuk semua γ < α.
Biarkan I(α, 0) menjadi kardinal pertama -lemah tidak dapat diakses, I(α, β+1) menjadi kardinal α-lemah tidak dapat diakses berikutnya setelah I(α, β), dan I(α, β) untuk limit ordinal &space;=&space;\textup{sup}\left&space;\{&space;I(\alpha,&space;\gamma)&space;\mid&space;\gamma&space;%3C&space;\beta&space;\right&space;\}) .
.
Di bagian ini variabel I(α, 0), dicadangkan untuk kardinal biasa yang tak terhitung jumlahnya dari bentuk atau I(α, β+1).
Kemudian,
- Predikat ANF;
- Himpunan TA yaitu himpunan ordinal yang dapat dihitung sehingga setiap elemen himpunan dapat dilambangkan secara unik hanya dengan menggunakan simbol 0, +, I, ψ di mana ψ menunjukkan hierarki fungsi yang runtuh α-kardinal yang tidak dapat diakses dengan lemah;
- Himpunan PA (Subset TA yang hanya mencakup bilangan pokok tambahan).
Barisan dasar untuk bilangan urut α dengan kofinalitas cof(α) = β adalah barisan yang meningkat secara ketat (α[η])η<β dengan panjang β dan dengan limit α, di mana α[η] adalah elemen ke-η dari urutan ini.
H. Fungsi Runtuh dengan Lemah Kardinal Mahlo (The Functions Collapsing Weakly Mahlo Cardinals)
1. Definisi
Sebuah ordinal adalah Mahlo lemah jika itu adalah kardinal reguler yang tak terhitung, dan kardinal reguler di dalamnya (dengan kata lain, kurang dari itu) tidak bergerak.
Pada bagian ini variabel ρ, π dicadangkan untuk kardinal reguler yang tak terhitung dari bentuk ) atau
atau  .
.
Dimana R menunjukkan kelas dari semua kardinal biasa yang Tak Terhitung dan W menunjukkan kelas dari semua kardinal Mahlo yang lemah.
I. Urutan Dasar untuk Fungsi yang Runtuh α-kardinal Mahlo yang Lemah (Fundamental Sequences for the Function Collapsing α-Weakly Mahlo Cardinals)
1. Definisi M(α;β)
Jika β = 0 atau β = β'+1 maka M(α;β) adalah kardinal Mahlo α-lemah.
Biarkan pada halaman ini ) adalah himpunan semua kardinal Mahlo α-lemah, R adalah himpunan semua kardinal reguler tak terhitung yang kurang dari
adalah himpunan semua kardinal Mahlo α-lemah, R adalah himpunan semua kardinal reguler tak terhitung yang kurang dari &space;\right&space;\}) dan variabel π dicadangkan untuk kardinal reguler tak terhitung dari bentuk
dan variabel π dicadangkan untuk kardinal reguler tak terhitung dari bentuk ) atau
atau ) .
.
3. Urutan Dasar (Fundamental Sequences)
Barisan fundamental untuk Ordinal limit A yang dapat dihitung didefinisikan sebagai berikut :
J. Urutan Dasar untuk OCF menggunakan Kardinal Kompak Lemah (Weakly Compact Cardinal)
1. Definisi
Biarkan K menunjukkan kardinal yang kompak lemah, Ω0 = 0 dan Ωα adalah kardinal ke-α yang tak terhitung. Kemudian,
2. Urutan Dasar (Fundamental Sequences)
Untuk notasi yang menggunakan barisan fundamental kardinal kompak lemah didefinisikan sebagai berikut :
Sistem barisan fundamental ini dapat didefinisikan dari konsep teori-bukti yang dikenal sebagai "norma".
Berikut, inilah Sumber-sumber lainnya dari beberapa Tautan di bawah ini :
- https://googology.wikia.org/wiki/User_blog:Hyp_cos/Degrees_of_Recursive_Inaccessibility_and_other_OCFs
- https://googology.wikia.org/wiki/User_blog:Denis_Maksudov/Slowly_growing_ordinal_function_and_FS_up_to_BHO.
- https://googology.wikia.org/wiki/User_blog:Denis_Maksudov/FS_for_Hypcos%27s_notation_(with_weakly_inaccessibles_cardinals)_up_to_%CE%A8(M%5E2)
- https://googology.wikia.org/wiki/User_blog:Denis_Maksudov/My_system_of_number_names_(Fast_Growing_Series,_FGS)
- https://googology.wikia.org/wiki/User_blog:Hyp_cos/extended_Kruskal_theorem
- https://googology.wikia.org/wiki/User_blog:Deedlit11/Ordinal_Notations_V:_Up_to_a_weakly_Mahlo_cardinal
- https://googology.wikia.org/wiki/User_blog:Denis_Maksudov/OCF_and_ordinal_notation_based_on_a_weakly_Mahlo_cardinal
GENERALISASI FUNGSI RUNTUH ORDINAL (ORDINAL COLLAPSING FUNCTIONS GENERALIZATIONS) [PART 1]
A. Fungsi Runtuh Ordinal (Ordinal Collapsing Functions)
Sebelum itu, marilah kita perkenalkan terlebih dahulu tentang Fungsi Runtuh Ordinal atau disebut juga sebagai Ordinal Collapsing Functions.
B. Perbandingan antara Ketiga Fungsi Runtuh Ordinal (Comparison between the Three Ordinal Collapsing Functions)
Di bawah ini merupakan Perbandingan antara Ketiga Fungsi Runtuh Ordinal (Ordinal Collapsing Functions) :
1. Dari 1 sampai ε0
2. Dari ε0 sampai SVO
5. Dari θ(ζΩ+1,0) sampai θ(Ω2,0)
6. Dari θ(Ω2, 0) sampai θ(Ω2 ^ Ω2, 0)
7. Dari θ(Ω2 ^ Ω2, 0) sampai θ(εΩ_2+1, 0)
11. Dari θ(Ω3 ^ Ω3, 0) sampai θ(εΩ_3+1, 0)
16. Dari ψ0(Ωω) sampai ψ0(Ωω ^ Ωω)
18. Dari ψ0(Ωω ^ Ωω ^ Ω) sampai ψ0(Ωω+1)
C. Analisis Generalisasi Limit Ordinal Runtuh (OCF) Orde 0 dan 1
Berikut, inilah beberapa Analisis Generalisasi dari Limit Ordinal (OCF) Orde 0 dan 1 :
1. Generalisasi Ordinal dari ε0 ke ε1
25. Generalisasi Ordinal dari ϑ(Ωϑ(Ω^2)) ke ϑ(Ωϑ(Ω^2)+1)
GENERALISASI KARDINAL MAHLO YANG TAK DAPAT DIAKSES (GENERALIZATION OF INACCESSIBLE MAHLO'S CARDINAL [PART 2]
A. Generalisasi Kardinal Mahlo
Di bawah ini merupakan Generalisasi Kardinal Mahlo yang Tak dapat Diakses (Generalizations of Inaccessible Mahlo's Cardinal) :
1. Dari 1 sampai ψ(M)
B. Analisis Generalisasi Fungsi Runtuh Ordinal berdasarkan Kardinal Mahlo
Di bawah ini merupakan beberapa Analisis Generalisasi Fungsi Runtuh Ordinal (Ordinal Collapsing Functions) berdasarkan dengan Kardinal Mahlo :
1. Dari 1 sampai ε0
2. Dari ε0 sampai SVO
3. Dari SVO sampai BHO
4. Dari BHO sampai ψ0(Ω2 ^ 2 * 2)
5. Dari ψ0(Ω2 ^ 2 * 2) sampai ψ0(Ω2 ^ Ω2)
6. Dari ψ0(Ω2 ^ Ω2) sampai ψ0(Ω2 ^ Ω2 ^ Ω2)
7. Dari ψ0(Ω2 ^ Ω2 ^ Ω2) sampai ψ0(Ω3)
9. Dari ψ0(Ω3 ^ ω) sampai ψ0(Ω3 ^ Ω3)
17. Dari ψ0(Ωω ^ Ωω) sampai ψ0(Ωω ^ Ωω ^ Ω)
18. Dari ψ0(Ωω ^ Ωω ^ Ω) sampai ψ0(Ωω+1)
19. Dari ψ0(Ωω+1) sampai ψ0(Ωω+1 ^ Ωω+1)
20. Dari ψ0(Ωω+1 ^ Ωω+1) sampai ψ0(Ωω+2)
21. Dari ψ0(Ωω+2) sampai ψ0(Ωω+3)
22. Dari ψ0(Ωω+3) sampai ψ0(Ωω2)
LEVEL FUNGSI RUNTUH ORDINAL (ORDINAL COLLAPSING FUNCTIONS LEVELS)
Artikel lainnya : Googology.wikia.org (OCF vs Array Notation)
1. Kardinal Pertama Tak Terhitung (First Uncountable Cardinals)
Sekarang kita perlu memikirkan sesuatu yang disebut "Kofinalitas" - pada dasarnya, cara kerjanya seperti ini: Setiap kardinal (ω = ψ(1) dan Ω di bagian awal) memiliki kofinalitas yang sama dengan dirinya sendiri. 0 dan suksesor memiliki kofinalitas 0. α+β, αβ, dan αβ memiliki kofinalitas sama dengan β (kecuali jika β adalah 0, dalam hal ini α+0 memiliki kofinalitas α dan yang lainnya memiliki kofinalitas 0). ψ(0) memiliki kofinitas 0 dan ψ(α) untuk semua α lainnya memiliki kofinalitas ω.
Untuk mendefinisikan FS untuk ordinal dengan kofinalitas Ω, yang terbaik adalah menganggapnya sebagai output dari beberapa fungsi f(Ω). Contohnya, ΩΩ2 = f(Ω), dimana f didefinisikan sebagai f(α) = ΩΩ+α. Ini pada dasarnya sama dengan FSes normal, tetapi dengan alih-alih Ω[n] di akhir ω[n].
Kita kemudian dapat mengatakan bahwa, jika ordinal memiliki kofinalitas Ω :
2. Kardinal Tak Terhitung Tertinggi (Higher Uncountable Cardinals)
Kami sekarang memperkenalkan kardinal Ωα. Pertama, membantu memperkenalkan konsep "Kardinal Penerus". Kardinal Suksesor/Penerus Ωα adalah Ωα+1. Kita juga perlu memperkenalkan "kardinalitas", yang merupakan kardinal tertinggi dalam sebuah ekspresi. Jadi kardinalitas dari, katakanlah  adalah Ω2.
adalah Ω2.
Satu hal penting lainnya yang perlu diperhatikan yaitu jika α bukan penerus, Ωα memiliki Kofinalitas sama dengan α. Jadi ΩΩ memiliki kofinalitas Ω.
Inilah aturan umum untuk menangani kardinal yang runtuh dengan kofinalitas Ωα, ditulis sebagai f(Ωα).
Anda akan melihat bahwa kami mendefinisikan fungsi ψα untuk kardinal yang lebih tinggi. Cara kerjanya adalah ψα pada fungsi α kolaps, adalah kardinal pertama yang mendiagonalisasi; semua kardinal yang lebih rendah darinya mengikuti aturan FS (karena akan memiliki kofinalitas yang lebih besar). Juga, ψα(0) adalah kardinal yang kardinal penggantinya adalah α. Misalnya :
Catatan: Terkadang, ψn digunakan. Ini sebenarnya sesuai dengan fungsi . Singkatan ini umum digunakan dan diperbolehkan (kecuali jika akan bertentangan dengan notasi normal).
Berikut adalah beberapa contoh nilai dengan OCF dengan Ω2 kardinal. Konsep serupa berlaku pada kardinal yang lebih tinggi dan limitnya sama dengan OCF normal.
3. Inaccessibles (Tak dapat diakses)
Kami sekarang memperkenalkan kardinal I yang tidak dapat diakses, sebagai pendiagonalisasi dari Ωα. Hal-hal dengan kofinalitas saya dekomposisi dengan cara yang sama seperti sebelumnya, ke sarang fungsi ψα. Berikut cara kerja fungsi ψα :
Jadi berikut adalah beberapa ordinal yang ditulis hanya dengan fungsi ψI (sebagai UNOCF = OCF normal) :
Pada ψ(Iω), kami mencapai titik di mana kami telah mengejar OCF normal. Setelah ini kita dapat memiliki hal-hal seperti ψ(II), dll.
Pada titik ini kita perlu mendefinisikan "kardinal pengganti" dari I. Itu mudah - itu ΩI+1. Kemudian kita dapat memiliki penerus lebih lanjut dan, akhirnya membatasi kardinal. Berikut adalah beberapa contoh bagaimana ini digunakan :
Sekarang kita mencapai hal serupa yang mengarah pada pencapaian I, dan kita membutuhkan kardinal lain yang tidak dapat diakses. Kami menggunakan I2 untuk mewakili ini.
Sekarang kita dapat membuat barisan diagonalsasi ordinal. Kami akan terus menggunakan I untuk menunjukkan setiap fungsi.
Sebagai contoh :
5. Memperkenalkan Mahlo
Dalam beberapa hal, fungsi I terlihat seperti Fungsi Veblen φ, dan kita membutuhkan cara untuk mendiagonalisasinya. Di sinilah kardinal Mahlo M dan fungsi ψM masuk.
ψM(α) tetap Ω1+α. Tapi ψM(M) tetap I. Faktanya, M pada dasarnya membuat diagonalisasi dari benda yang digantikannya. Berikut adalah lebih banyak contoh nilai fungsi ψM :
6. Kardinal Mahlo yang lebih tinggi
Pada titik ini, kita perlu mendiagonalisasi ini, dan kita dapat melakukannya dengan kardinal Mahlo lain yaitu M2, dan fungsi  . Berikut cara kerja fungsi
. Berikut cara kerja fungsi  :
:
Faktanya, aturan umum yang sama berlaku untuk ekspresi M ini seperti untuk ekspresi yang setara dengan Ω - cukup ganti semua Ω dengan M dan Anda siap melakukannya.
7. Kardinal Mahlo ke-2 (2-Mahlo Cardinals)
Pada titik ini, kita perlu mendiagonalisasi kardinal Mahlo, dengan cara yang sama Mahlos mendiagonalisasi kardinal biasa dan tidak dapat diakses. Untuk melakukan ini, kami memperkenalkan N, kardinal 2-Mahlo, dengan Mahlos biasa menjadi 1-Mahlo. Berikut cara menggunakan fungsinya ψN :
8. Fungsi C (Kardinal Mahlo ke-n & Hyper-Mahlo)
Pada titik ini, kami membuat pola. M mendiagonalisasi atas kardinal biasa, dan N mendiagonalisasi atas Mahlos. Jadi kita perlu sesuatu untuk menggeneralisasi prosedur ini.
Pada titik ini, mari kita perkenalkan fungsi yang akan saya kembangkan selama beberapa bagian berikutnya - fungsi C, C adalah singkatan dari kardinal. Pada dasarnya, ini mewakili semua lapisan kardinal yang telah kita definisikan, dengan C(0; x) menjadi kardinal normal, C(1; x) menjadi Mahlos, dan C(2; x) menjadi 2-Mahlos (berbasis N. Intinya, bagian array dari fungsi C membuat diagonalisasi titik tetap, sedangkan bagian sebelum titik koma adalah level, dengan setiap pendiagonalisasi level di atas yang sebelumnya.) Misalnya :
9. Kardinal Kompak Lemah (Weakly Compact Cardinal)
Sekarang kita membutuhkan kardinal baru yang lebih tinggi untuk mendiagonalisasi tingkat kardinal Mahlo. Kami menggunakan kardinal kompak lemah, K. Berikut cara kerja fungsi ψK :
10. Lebih Kompak, dan Tiga Argumen Fungsi C
11. Tahap yang lebih tinggi dan Fungsi C umum
Pada titik ini, akan sangat membantu untuk membagi kardinal yang telah kita buat menjadi "tahapan" - Ω dan I biasa adalah "tahap 1", M adalah "tahap 2" dan K adalah "tahap 3". Jadi, untuk mendiagonalisasi lebih lanjut kita membutuhkan tingkat kardinal yang lebih tinggi. saya akan menyebutnya sebagai "tahap n" dan hanya menggunakan fungsi C umum.
12. Kardinal Panggung (Stage Cardinal)
Anda mungkin telah memperhatikan bahwa fungsi C lebih mirip fungsi Veblen, dan kita memerlukan beberapa cara untuk mendiagonalisasinya. Karena itu saya akan memperkenalkan kardinal besar baru, yang disebut kardinal panggung, T. ψT menghasilkan kardinal seperti ini :
13. Lebih banyak Kardinal Panggung (More Stage Cardinals)
Sekarang, kita perlu mendefinisikan kardinal tahap kedua, T2. Ini bekerja dengan cara yang sangat mirip dengan T, tetapi dimulai dari T alih-alih Ω - jadi :
15. Lebih banyak Kardinal Titik Koma Ganda
16. Kardinal Metapanggung/Metatahap (Metastage Cardinal) dan Tiga Titik Koma
Sekarang, kita perlu membuat kardinal baru yang disebut X, atau Kardinal Metatahap (Metastage Cardinal). X bekerja dengan cara yang mirip dengan T, tetapi berdasarkan titik koma ganda, bukan titik koma normal. Jadi :
17. Meta^n-tahap, Beberapa Titik Koma, dan Ordinal Menjatuhkan Kecil (Small Dropping Ordinal)
Adapun Aturan-aturan yang perlu kita ketahui dalam Menjatuhkan Fungsi Runtuh Ordinal (Dropping Ordinal Collapsing Functions) yaitu :
GENERALISASI LEVEL FUNGSI RUNTUH ORDINAL (GENERALIZATION OF ORDINAL COLLAPSING FUNCTIONS LEVELS) [PART 3]
Di bawah ini merupakan Generalisasi Level Fungsi Runtuh Ordinal (Generalizations of Ordinal Collapsing Function Levels) dari Skala 1 sampai 2 :
1. Generalisasi Ordinal dari ψ0(Ω) ke ψ0(Ω2)
2. Generalisasi Ordinal dari ψ0(M) ke ψ0(M2)
3. Generalisasi Ordinal dari ψ0(T) ke ψ0(T2)
4. Generalisasi Ordinal dari ψ0(X) ke ψ0(X2)
5. Generalisasi Ordinal dari ψ0(Y) = ψ0(C(1;;;; 0)) ke ψ0(Y2) = ψ0(C(1;;;; 1))
6. Generalisasi Ordinal dari ψ0(C(1{5}0)) ke ψ0(C(1{5}1))
7. Generalisasi Ordinal dari ψ0(C(1{ω}0)) ke ψ0(C(1{ω}1))
8. Generalisasi Ordinal dari ψ0(C(1{ω+1}0)) ke ψ0(C(1{ω+1}1))
9. Generalisasi Ordinal dari ψ0(C(1{ω2}0)) ke ψ0(C(1{ω2}1))
10. Generalisasi Ordinal dari ψ0(C(1{Ω}0)) ke ψ0(C(1{Ω}1))
11. Generalisasi Ordinal dari ψ0(C(1{M}0)) ke ψ0(C(1{M}1))
12. Generalisasi Ordinal dari ψ0(C(1{K}0)) ke ψ0(C(1{K}1))
13. Generalisasi Ordinal dari ψ0(C(1{C(1{ω}0)}0)) ke ψ0(C(1{C(1{ω}0)}1))
B
14. Generalisasi Ordinal dari ψ0(C(1{1, 0}0)) ke ψ0(C(1{1, 0}1))
15. Generalisasi Ordinal dari ψ0(C(1{1, 1}0)) ke ψ0(C(1{1, 1}1))
16. Generalisasi Ordinal dari ψ0(C(1{1, ω}0)) ke ψ0(C(1{1, ω}1))










 disebut derajat α, dan memenuhi
disebut derajat α, dan memenuhi  dalam bentuk normal Cantor, dan membuat asumsi yang sama untuk
dalam bentuk normal Cantor, dan membuat asumsi yang sama untuk 

 dalam bentuk normal Cantor dan
dalam bentuk normal Cantor dan 



 , dst. Pada perbedaan pertama, ordinal yang memiliki komponen lebih besar adalah ordinal yang lebih besar. Jika mereka sama sampai yang satu berakhir sebelum yang lain, maka yang berakhir lebih dulu lebih kecil.
, dst. Pada perbedaan pertama, ordinal yang memiliki komponen lebih besar adalah ordinal yang lebih besar. Jika mereka sama sampai yang satu berakhir sebelum yang lain, maka yang berakhir lebih dulu lebih kecil.


























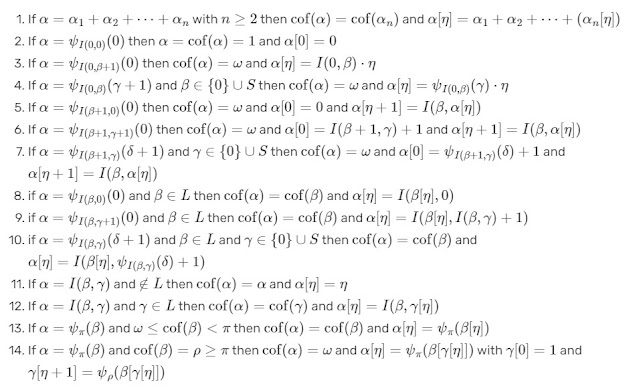













,0).jpg)
















)%20to%20%CF%88(%CE%A9_(%CF%89+3)).jpg)


































































































.jpeg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20%CE%A9%20to%20%CE%A9_2.jpg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20M%20to%20M_2.jpg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20T%20to%20T_2.jpg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20X%20to%20X_2.jpg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20Y%20to%20Y_2.jpg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20C(1%7B5%7D0)%20to%20C(1%7B5%7D1).jpg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20C(1%7B%CF%89%7D0)%20to%20C(1%7B%CF%89%7D1).jpg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20C(1%7B%CF%89+1%7D0)%20to%20C(1%7B%CF%89+1%7D1).jpg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20C(1%7B%CF%892%7D0)%20to%20C(1%7B%CF%892%7D1).jpg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20C(1%7B%CE%A9%7D0)%20to%20C(1%7B%CE%A9%7D1).jpg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20C(1%7BM%7D0)%20to%20C(1%7BM%7D1).jpg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20C(1%7BK%7D0)%20to%20C(1%7BK%7D1).jpeg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20C(1%7BC(1%7B%CF%89%7D0)%7D0)%20to%20C(1%7BC(1%7B%CF%89%7D0)%7D1).jpeg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20C(1%7B1,%200%7D0)%20to%20C(1%7B1,%200%7D1).jpeg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20C(1%7B1,%201%7D0)%20to%20C(1%7B1,%201%7D1).jpg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20C(1%7B1,%20%CF%89%7D0)%20to%20C(1%7B1,%20%CF%89%7D1).jpg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20C(1%7B2,%200%7D0)%20to%20C(1%7B2,%200%7D1).jpg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20C(1%7B1,%200,%200%7D0)%20to%20C(1%7B1,%200,%200%7D1).jpg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20C(1%7B1,%200,%200,%200%7D0)%20to%20C(1%7B1,%200,%200,%200%7D1).jpg)
%5D%20Generalizations%20of%20Ordinal%20Collapsing%20Function%20from%20C(1%7B1;%200%7D0)%20to%20C(1%7B1;%200%7D1).jpg)