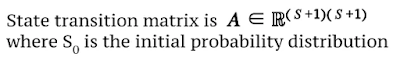Assalamu‘alaikum wr. wb.
Halo gais! Jika sebelumnya sudah membahas tentang Reinforcement Learning dalam AI dan Machine Learning. Sekarang, waktunya membahas tentang Naïve-Bayes Algorithm dan Hidden Markov Model.
 |
| Ilustrasi Pemodelan dari Algoritma Naive-Bayes dan Hidden Markov |
NAIVE-BAYES ALGORITHM
Sumber Materi : en.Wikipedia.org, Scikit-Learn.org, Javatpoint.com, Geeksforgeeks.org, Kdnuggets.com, dan Analytics Vidhya
A. Pengertian dan Klasifikasi dari Algoritma Naïve-Bayes
Solusi yang paling sederhana biasanya adalah yang paling kuat, dan Naïve Bayes adalah contoh yang baik untuk itu. Meskipun kemajuan dalam Pembelajaran Mesin dalam beberapa tahun terakhir, Naïve Bayes terbukti tidak hanya sederhana tetapi juga cepat, akurat, dan dapat diandalkan.
Ini telah berhasil digunakan untuk banyak tujuan, tetapi bekerja sangat baik dengan masalah Pemrosesan Bahasa Alami (NLP).
Naïve Bayes adalah algoritma pembelajaran mesin probabilitas berdasarkan Teorema Bayes, digunakan dalam berbagai tugas klasifikasi. Dalam artikel ini, kita akan memahami algoritma Naïve Bayes dan semua konsep penting sehingga tidak ada ruang bagi keraguan dalam pemahaman.
Teorema Bayes adalah rumus matematika sederhana yang digunakan untuk menghitung probabilitas bersyarat.
Probabilitas bersyarat adalah ukuran probabilitas terjadinya suatu peristiwa yang diberikan bahwa peristiwa lain telah terjadi (berdasarkan asumsi, dugaan, assersi, atau bukti).
Adapun Klasifikasi dari Algoritma Naïve Bayes, yaitu sebagian berikut :
- Algoritma Naïve Bayes adalah algoritma pembelajaran terawasi, yang didasarkan pada teorema Bayes dan digunakan untuk memecahkan masalah klasifikasi.
- Algoritma ini terutama digunakan dalam klasifikasi teks yang melibatkan dataset pelatihan berdimensi tinggi.
- Klasifikasi Naïve Bayes adalah salah satu algoritma Klasifikasi yang sederhana dan paling efektif yang membantu dalam membangun model pembelajaran mesin yang cepat dan dapat melakukan prediksi dengan cepat.
- Ini adalah klasifikasi probabilitas, yang berarti ia memprediksi berdasarkan probabilitas suatu objek.
- Beberapa contoh populer dari Algoritma Naïve Bayes adalah filtrasi spam, analisis sentimen, dan klasifikasi artikel.
Mengapa disebut dengan Naïve Bayes?
Algoritma Naïve Bayes terdiri dari dua kata Naïve dan Bayes, yang dapat digambarkan sebagai :
- Naïve : Disebut Naïve karena mengasumsikan bahwa kemunculan fitur tertentu tidak bergantung pada kemunculan fitur lainnya. Seperti jika buah diidentifikasi berdasarkan warna, bentuk, dan rasa, maka buah merah, bulat, dan manis dikenali sebagai buah apel. Karenanya setiap fitur secara individual berkontribusi untuk mengidentifikasi bahwa itu adalah sebuah apel tanpa saling bergantung satu sama lain.
- Bayes : Disebut Bayes karena bergantung pada prinsip Teorema Bayes.
B. Kelebihan dan Kekurangan dari Naïve-Bayes
Inilah beberapa Kelebihan dan Kekurangan Naive Bayes.
Kelebihan :
- Mudah dan cepat dalam memprediksi kelas dari set data uji. Juga memberikan kinerja yang baik dalam prediksi multi kelas.
- Ketika asumsi independensi terpenuhi, klasifikasi dilakukan dengan lebih baik dibandingkan dengan model pembelajaran mesin lain seperti regresi logistik atau pohon keputusan, dan membutuhkan jumlah data pelatihan yang lebih sedikit.
- Kinerjanya baik dalam kasus variabel input kategorikal dibandingkan dengan variabel numerik. Untuk variabel numerik, diasumsikan bahwa distribusinya normal (kurva lonceng), yang merupakan asumsi yang kuat.
Kekurangan :
- Jika variabel kategorikal memiliki kategori (di set data uji) yang tidak diamati dalam set data pelatihan, maka model akan memberikan probabilitas 0 (nol) dan tidak dapat melakukan prediksi. Hal ini sering disebut "Frekuensi Nol". Untuk mengatasi hal ini, kita dapat menggunakan teknik smoothing. Salah satu teknik smoothing paling sederhana adalah yang disebut estimasi Laplace.
- Di sisi lain, Naive Bayes juga dikenal sebagai estimator yang buruk, sehingga keluaran probabilitas dari predict_proba tidak perlu dianggap terlalu serius.
- Keterbatasan lain dari algoritma ini adalah asumsi prediktor yang independen. Dalam kehidupan nyata, hampir tidak mungkin mendapatkan set prediktor yang benar-benar independen.
C. Penerapan dari Naïve-Bayes
Naïve-Bayes adalah algoritma klasifikasi yang populer dan banyak digunakan dalam berbagai aplikasi di kehidupan sehari-hari. Berikut ini adalah beberapa contoh penerapan Naïve-Bayes dalam konteks sehari-hari:
1. Filtering Email Spam
Naïve-Bayes sering digunakan dalam filter spam email. Dengan melatih model Naïve-Bayes menggunakan dataset email yang dikategorikan sebagai spam atau bukan spam, algoritma ini dapat mempelajari pola dari email yang cenderung spam dan dapat secara efektif memfilter email yang masuk ke kotak masuk kita.
2. Klasifikasi Dokumen
Naïve-Bayes dapat digunakan untuk mengklasifikasikan dokumen ke dalam kategori yang sesuai. Misalnya, dalam sistem manajemen dokumen, Naïve-Bayes dapat digunakan untuk mengkategorikan dokumen sebagai berita, artikel, atau laporan berdasarkan isinya.
3. Deteksi Sentimen
Naïve-Bayes dapat digunakan untuk menganalisis sentimen dalam teks, seperti pada analisis sentimen di media sosial. Dengan melatih model Naïve-Bayes menggunakan dataset teks yang dikategorikan sebagai positif, negatif, atau netral, algoritma ini dapat memprediksi sentimen dari teks yang baru.
4. Pengklasifikasian Produk
Naïve-Bayes juga dapat digunakan dalam sistem pengklasifikasi produk, seperti pengklasifikasi berita, film, atau produk online. Dengan melatih model menggunakan dataset produk yang telah dikategorikan, Naïve-Bayes dapat membantu pengguna dalam memilih produk yang sesuai dengan preferensi mereka.
5. Deteksi Penipuan Keuangan
Naïve-Bayes dapat digunakan untuk deteksi penipuan keuangan, seperti dalam transaksi kartu kredit. Dengan melatih model menggunakan dataset transaksi yang dikategorikan sebagai penipuan atau bukan, Naïve-Bayes dapat membantu mengidentifikasi pola transaksi yang mencurigakan dan memberi peringatan kepada pihak yang berwenang.
6. Analisis Sentimen pada Ulasan Produk
Naïve-Bayes dapat digunakan untuk menganalisis sentimen pada ulasan produk di platform e-commerce. Dengan melatih model menggunakan dataset ulasan yang dikategorikan sebagai positif, negatif, atau netral, Naïve-Bayes dapat membantu pengguna dalam memahami umpan balik pelanggan terhadap produk tertentu.
7. Klasifikasi Bahasa
Naïve-Bayes dapat digunakan dalam klasifikasi bahasa, misalnya dalam sistem penerjemahan mesin. Dengan melatih model menggunakan dataset teks dalam berbagai bahasa, Naïve-Bayes dapat membantu mengenali bahasa yang digunakan dalam teks yang diberikan.
8. Klasifikasi Dokumen Medis
Naïve-Bayes dapat digunakan dalam klasifikasi dokumen medis, seperti membedakan antara catatan medis yang mengandung diagnosis penyakit tertentu atau tidak. Dengan melatih model menggunakan dataset dokumen medis yang telah dikategorikan, Naïve-Bayes dapat membantu dalam analisis dan pengklasifikasian dokumen medis.
9. Pengenalan Tulisan Tangan
Naïve-Bayes dapat digunakan dalam pengenalan tulisan tangan, seperti dalam sistem pengenalan karakter tulisan tangan pada cek atau dokumen penting lainnya. Dengan melatih model menggunakan dataset tulisan tangan yang dikategorikan, Naïve-Bayes dapat membantu dalam pengenalan karakter tulisan tangan dengan tingkat akurasi yang baik.
10. Deteksi Berita Palsu
Naïve-Bayes dapat digunakan dalam deteksi Berita Palsu (Hoaks). Dengan melatih model menggunakan dataset berita yang terverifikasi sebagai benar atau palsu, Naïve-Bayes dapat membantu dalam membedakan antara berita yang sahih dan berita palsu berdasarkan fitur-fitur yang ada dalam teks berita.
D. Rumus Teorema Naïve-Bayes
1. Teorema Bayes
Teorema Bayes menemukan probabilitas suatu peristiwa terjadi mengingat probabilitas peristiwa lain yang telah terjadi. Teorema Bayes dinyatakan secara matematis sebagai persamaan berikut :
Dimana :
- P(A|B) adalah Probabilitas Posterior : Probabilitas hipotesis A terjadi mengingat kejadian yang diamati B.
- P(B|A) adalah Probabilitas Kemungkinan : Probabilitas bukti diberikan bahwa probabilitas hipotesis benar.
- P(A) adalah Probabilitas Sebelumnya : Probabilitas hipotesis sebelum mengamati bukti.
- P(B) adalah Probabilitas Marginal : Probabilitas Bukti.
Sekarang, sehubungan dengan dataset kami, kami dapat menerapkan Teorema Bayes dengan cara berikut :
Di mana, y adalah variabel kelas dan X adalah vektor fitur dependen (berukuran n) di mana :
X = (x1, x2, x3, …, xn)
2. Asumsi Naïve
Sekarang saatnya untuk menempatkan asumsi naif pada teorema Bayes, yaitu independensi di antara fitur-fiturnya. Jadi sekarang, kami membagi bukti menjadi bagian-bagian independen.
Sekarang, jika dua kejadian A dan B saling bebas, maka :
Oleh karena itu, kita telah mencapai hasil :
Yang dapat dinyatakan sebagai :
Sekarang, karena penyebutnya tetap konstan untuk input yang diberikan, kita dapat menghapus suku tersebut :
Sekarang, kita perlu membuat model classifier. Untuk ini, kami menemukan probabilitas set input yang diberikan untuk semua nilai yang mungkin dari variabel kelas y dan mengambil output dengan probabilitas maksimum. Ini dapat dinyatakan secara matematis sebagai :
Jadi, akhirnya, kita tinggal menghitung P(y) dan P(xi | y).
Perhatikan bahwa P(y) juga disebut probabilitas kelas dan P(xi | y) disebut probabilitas bersyarat.
Pengklasifikasi Naive Bayes yang berbeda berbeda terutama oleh asumsi yang mereka buat mengenai distribusi P(xi | y).
3. Gaussian Naïve-Bayes Classifier
Dalam Gaussian Naive Bayes, nilai kontinu yang terkait dengan setiap fitur diasumsikan terdistribusi menurut distribusi Gaussian. Distribusi Gaussian disebut juga distribusi Normal. Ketika diplot, akan memberikan kurva berbentuk lonceng yang simetris terhadap rata-rata nilai fitur seperti yang ditunjukkan di bawah ini :
Tabel yang diperbarui dari probabilitas sebelumnya untuk fitur prospek adalah sebagai berikut.
Kemungkinan fitur diasumsikan sebagai Gaussian, karenanya, probabilitas bersyarat diberikan oleh :
E. Contoh Soal Naïve-Bayes
Misalkan kita memiliki dataset kondisi cuaca dan variabel target yang sesuai "Bermain". Jadi dengan menggunakan dataset ini kita perlu memutuskan apakah kita harus bermain atau tidak pada hari tertentu sesuai dengan kondisi cuaca. Jadi untuk mengatasi masalah ini, kita perlu mengikuti langkah-langkah di bawah ini :
- Ubah dataset yang diberikan menjadi tabel frekuensi.
- Hasilkan tabel Kemungkinan dengan menemukan probabilitas fitur yang diberikan.
- Sekarang, gunakan Teorema Bayes untuk menghitung probabilitas posterior.
Masalah : Jika cuaca cerah, apakah Player harus bermain atau tidak?
Solusi : Untuk mengatasi ini, pertama pertimbangkan dataset di bawah ini:
Cuaca | Main | |
1. | Hujan | Ya |
2. | Cerah | Ya |
3. | Mendung | Tidak |
4. | Mendung | Ya |
5. | Cerah | Tidak |
6. | Hujan | Ya |
7. | Cerah | Ya |
8. | Mendung | Ya |
9. | Hujan | Tidak |
10. | Cerah | Tidak |
11. | Cerah | Ya |
12. | Hujan | Tidak |
13. | Mendung | Ya |
14. | Mendung | Ya |
Tabel frekuensi untuk Kondisi Cuaca :
Cuaca | Ya | Tidak |
Mendung | 4 | 1 |
Hujan | 2 | 2 |
Cerah | 3 | 2 |
Total | 10 | 5 |
Kondisi cuaca tabel kemungkinan :
Cuaca | Ya | Tidak | Probabilitas |
Mendung | 4 | 1 | 5/14 = 0,36 |
Hujan | 2 | 2 | 4/14 = 0,29 |
Cerah | 3 | 2 | 5/14 = 0,35 |
Semua | 9 | 5 | |
Probabilitas | 9/14 = 0,29 | 10/14 = 0,71 |
Menerapkan Teorema Bayes :
- P(Ya|Cerah) = P(Cerah|Ya) * P(Ya) / P(Cerah)
- P(Cerah|Ya) = 3/10 = 0,3
- P(Cerah) = 0,35
- P(Ya) = 0,71
- Jadi, P(Ya|Cerah) = 0,3 * 0,71 / 0,35 = 0,60
- P(Tidak|Cerah) = P(Cerah|Tidak) * P(Tidak) / P(Cerah)
- P(Cerah|Tidak) = 2/4 = 0,5
- P(Tidak) = 0,29
- P(Cerah) = 0,35
- Jadi, P(No|Cerah) = 0,5 * 0,29 / 0,35 = 0,41
Sehingga seperti yang dapat kita lihat dari perhitungan di atas bahwa P(Ya|Cerah) > P(Tidak|Cerah)
F. Kode Program dari Naïve-Bayes (Dalam Python)
Untuk Kode Program Python dari Naive-Bayes, bisa menggunakan Library Scikit Learn yang dapat diakses di sini untuk melakukan Instalasi Library tersebut.
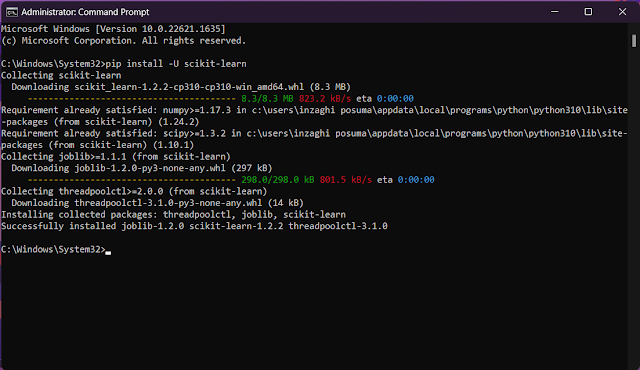
Pertama, ketiklah Perintah ini untuk melakukan Instalasi Scikit Learn :
pip install -U scikit-learn
Kemudian, dilanjutkan dengan mengetik :
python -m pip show scikit-learn # to see which version and where scikit-learn is installed python -m pip freeze # to see all packages installed in the active virtualenv
GaussianNB mengimplementasikan algoritma Gaussian Naïve Bayes untuk klasifikasi. Parameter σy dan μy diestimasi menggunakan kemungkinan maksimum.
from sklearn.datasets import load_irisfrom sklearn.model_selection import train_test_splitfrom sklearn.naive_bayes import GaussianNBX, y = load_iris(return_X_y=True)X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)gnb = GaussianNB()y_pred = gnb.fit(X_train, y_train).predict(X_test)print("Number of mislabeled points out of a total %d points : %d" % (X_test.shape[0], (y_test != y_pred).sum()))Number of mislabeled points out of a total 75 points : 4
Sekarang, kita melihat implementasi pengklasifikasi Gaussian Naive Bayes menggunakan scikit-learn.
| yes | no | P(yes) | P(no) | |
Sunny | 3 | 2 | 3/9 | 2/5 |
Overcast | 4 | 0 | 4/9 | 0/5 |
Rainy | 2 | 3 | 2/9 | 3/5 |
Total | 9 | 5 | 100% | 100% |
Kode Program pada Tabel di atas :
# Load the iris datasetfrom sklearn.datasets import load_irisfrom sklearn.model_selection import train_test_splitfrom sklearn.naive_bayes import GaussianNBfrom sklearn import metrics# Load the iris datasetiris = load_iris()# Store the feature matrix (X) and response vector (y)X = iris.datay = iris.target# Splitting X and y into training and testing setsX_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)# Training the model on training setgnb = GaussianNB()gnb.fit(X_train, y_train)# Making predictions on the testing sety_pred = gnb.predict(X_test)# Comparing actual response values (y_test) with predicted response values (y_pred)print("Gaussian Naive Bayes model accuracy (in %):", metrics.accuracy_score(y_test, y_pred) * 100)
Output :
Gaussian Naive Bayes model accuracy(in %) : 95.0
Anda juga bisa membuat Analisis Sentimen dalam Penelitian apapun ke dalam Metode Naive-Bayes, menggunakan Contoh Program Python di atas. Bisa menggunakan Python biasa maupun Jupyter Notebook.
HIDDEN-MARKOV MODEL
Sumber Materi : en.Wikipedia.org, Towardsdatascience.com (Medium.com), Nature.com
A. Pengertian dari Hidden Markov Model
Markov dan Hidden Markov Model dirancang untuk mengolah data yang dapat direpresentasikan sebagai 'urutan' pengamatan dari waktu ke waktu. Model Markov Tersembunyi merupakan kerangka kerja probabilistik di mana data yang diamati dimodelkan sebagai serangkaian keluaran yang dihasilkan oleh salah satu dari beberapa (tersembunyi) keadaan internal.
Sebagai bagian dari definisi, HMM mensyaratkan adanya proses Y yang dapat diamati yang hasilnya "dipengaruhi" oleh hasil X dengan cara yang diketahui. Karena X tidak dapat diamati secara langsung, tujuannya adalah mempelajari X dengan mengamati Y. HMM memiliki persyaratan tambahan bahwa hasil Y pada waktu t = t0 harus "dipengaruhi" secara eksklusif oleh hasil X pada t = t0 dan bahwa hasil dari X dan Y pada t < t0 harus bersyarat independen dari Y pada t = t0 diberikan X pada waktu t = t0.
B. Rumus-rumus dari Hidden Markov Model
Ketika kita tidak dapat mengamati keadaan itu sendiri tetapi hanya hasil dari beberapa fungsi probabilitas (pengamatan) dari keadaan tersebut, kita menggunakan HMM. HMM adalah model Markov statistik di mana sistem yang dimodelkan diasumsikan sebagai proses Markov dengan keadaan tidak teramati (tersembunyi).
- Model Markov : Serangkaian status (tersembunyi) z={z_1,z_2………….} diambil dari alfabet negara bagian S ={s_1,s_2,…….𝑠_|𝑆|} di mana z_i milik S.
- Hidden Markov Model : Serangkaian keluaran yang diamati x = {x_1,x_2,………} yang diambil dari alfabet keluaran V= {𝑣1, 𝑣2, . . , 𝑣_|𝑣|} di mana x_i milik V.
1. Asumsi Markov
a. Asumsi Horizon Terbatas : Probabilitas berada dalam keadaan pada waktu t hanya bergantung pada keadaan pada saat itu (t-1).
Itu berarti keadaan pada waktu t mewakili ringkasan masa lalu yang cukup untuk memprediksi masa depan. Asumsi ini adalah proses Markov Order-1. Proses Markov order-k mengasumsikan independensi bersyarat dari state z_t dari state yang k + 1 kali langkah sebelumnya.
b. Asumsi Proses Stasioner : Distribusi bersyarat (probabilitas) pada keadaan berikutnya, mengingat keadaan saat ini, tidak berubah dari waktu ke waktu.
Itu berarti negara terus berubah dari waktu ke waktu tetapi proses yang mendasarinya tidak bergerak.
2. Konvensi Notasi
- Ada keadaan awal dan pengamatan awal z_0 = s_0
- s_0 — distribusi probabilitas awal atas status pada waktu 0.
- Probabilitas keadaan awal — (π)
- pada t=1, kemungkinan melihat keadaan nyata pertama z_1 adalah p(z_1/z_0)
- Karena z0 = s0
3. Matriks Transisi Status
𝐀𝐢,𝐣 = Peluang transisi dari state i ke state j pada waktu t. Berikut adalah Matriks Transisi Status dari empat status termasuk status awal.
 |
| Matriks Transisi Status (State Transition Matrix) |
4. Probabilitas Urutan Tertentu
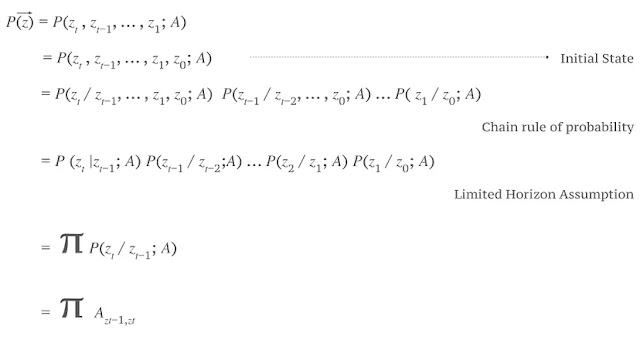 |
| Menemukan Probabilitas Urutan Tertentu |
C. Contoh Penerapan dari Hidden Markov Model
Contoh menggunakan
1. Prosedur Maju
S = {panas, dingin}
v = {v1=1 es krim, v2=2 es krim, v3=3 es krim} di mana V adalah Jumlah es krim yang dikonsumsi dalam sehari.
Contoh Urutan = {x1=v2, x2=v3, x3=v1, x4=v2}
 |
| (1) Diberikan Data sebagai Matriks |
 |
| (2) Mesin Finite State yang Dihasilkan untuk HMM |
Pertama, kita perlu menghitung probabilitas sebelumnya (yaitu, probabilitas menjadi panas atau dingin sebelum adanya pengamatan aktual). Ini dapat diperoleh dari S_0 atau π. Dari Gambar (1), S_0 diberikan sebagai 0,6 dan 0,4 yang merupakan probabilitas sebelumnya. Kemudian, berdasarkan asumsi Markov dan HMM, kita mengikuti langkah-langkah pada Gambar (3), Gambar (4), dan Gambar (5) di bawah ini untuk menghitung probabilitas urutan yang diberikan.
a. Untuk Keluaran Pertama yang diamati x1 = v2
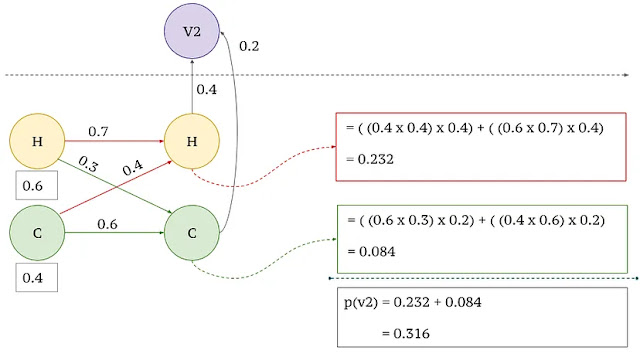 |
| (3) Langkah Pertama |
b. Untuk Output yang diamati x2=v3
 |
| (4) Langkah Kedua |
c. Untuk mengamati Output x3 dan x4
Demikian pula untuk x3=v1 dan x4=v2, kita harus mengalikan jalur yang mengarah ke v1 dan v2.
 |
| (5) Langkah Ketiga |
2. Penugasan Kemungkinan Maksimum
Untuk urutan keluaran yang diamati tertentu 𝑥 𝜖 𝑉_𝑇, kami bermaksud untuk menemukan rangkaian keadaan 𝑧 𝜖 𝑆_𝑇 yang paling mungkin. Kita dapat memahami ini dengan contoh yang ditemukan di bawah ini.
 |
| Contoh Data untuk Penugasan Kemungkinan Maksimum |
 |
| Markov Model as a Finite State Machine from |
Algoritma Viterbi adalah algoritma pemrograman dinamis yang mirip dengan prosedur maju yang sering digunakan untuk mencari kemungkinan maksimum. Alih-alih melacak probabilitas total untuk menghasilkan pengamatan, ia melacak probabilitas maksimum dan urutan keadaan yang sesuai.
Pertimbangkan urutan emosi : H,H,G,G,G,H selama 6 hari berturut-turut. Dengan menggunakan algoritme Viterbi, kami akan mengetahui lebih banyak kemungkinan seri tersebut.
 |
| Algoritma Viterbi Membutuhkan untuk memilih Jalur Terbaik |
Akan ada beberapa jalur menuju Sabtu cerah dan banyak jalur menuju Sabtu Hujan. Di sini kami bermaksud untuk mengidentifikasi jalur terbaik menuju Sabtu Cerah atau Hujan dan mengalikannya dengan probabilitas pancaran transisi Bahagia (karena Sabtu membuat orang tersebut merasa Bahagia).
Mari kita pertimbangkan Sabtu yang cerah. Hari sebelumnya (Jumat) bisa cerah atau hujan. Kemudian kita perlu mengetahui jalur terbaik hingga hari Jumat dan kemudian mengalikannya dengan probabilitas emisi yang berujung pada perasaan galau. Secara iteratif kita perlu mencari jalan terbaik di setiap hari yang berakhir dengan lebih banyak kemungkinan rangkaian hari.
 |
| Langkah 1 Penugasan Kemungkinan Maksimum dalam HMM |
 |
| Langkah 2 Penugasan Kemungkinan Maksimum dalam HMM |
 |
| Ulangi Algoritma untuk memilih Jalur Terbaik |
Algoritma memberi Anda nilai kemungkinan maksimum dan kami sekarang dapat menghasilkan urutan dengan kemungkinan maksimum untuk urutan keluaran yang diberikan.
3. Pelajari nilai untuk Parameter HMM A dan B
Pembelajaran dalam HMM melibatkan estimasi probabilitas transisi keadaan A dan probabilitas emisi keluaran B yang membuat urutan yang diamati paling mungkin. Algoritma Ekspektasi-Maksimalisasi digunakan untuk tujuan ini. Algoritma yang dikenal sebagai algoritma Baum-Welch, yang termasuk dalam kategori ini dan menggunakan algoritma maju, banyak digunakan.
Itulah Materi tentang Naive-Bayes Algorithm dan Hidden Markov Model dalam Machine Learning (ML) dan Kecerdasan Buatan (AI). Untuk melihat Materi tentang Probabilitas (Peluang) di Pelajaran Matematika SMA, silakan lihat di sini.
Mohon maaf apabila ada kesalahan apapun. Terima Kasih 😄😘👌👍 :)
Wassalamu‘alaikum wr. wb.

.png)

%20Scikit%20Learn%20Packages%20Installed%20Library%20Version%20in%20CMD.png)