Materi tentang Interpolasi dan Ekstrapolasi dalam Curve Fitting (+ Video Materi)

Assalamu‘alaikum wr. wb.

Halo gais! Dalam Metode Numerik, kita telah mengenal dari Akar-akar Persamaan Non-Linear dan juga Metode Simpleks. Kali ini, kita akan membahas tentang Rumus Interpolasi dan Ekstrapolasi dalam Curve Fitting.

Ilustrasi Interpolasi dan Ekstrapolasi dalam Curve Fitting

Sumber Materi : Dosenpendidikan.co.id, Plotly.com, Bookdown.org (Chapter 8 Interpolasi dan Ekstrapolasi), Fairuzelsaid.wordpress.com (Interpolasi Lagrange), dan Nyongcahfisika.wordpress.com

Sumber Kode Program : ChatGPT

MATERI

Interpolasi dalam Matematika Metode Numerik merujuk pada estimasi nilai tengah dari sejumlah nilai yang telah diketahui. Sedangkan secara umum, interpolasi adalah usaha untuk mendefinisikan fungsi yang mendekati suatu fungsi analitik yang tidak diketahui atau menggantikan fungsi yang rumit dengan fungsi yang dapat didefinisikan secara analitik.

Masalah umum dalam interpolasi adalah menemukan fungsi yang mendekati data yang ada, dan salah satu metodenya adalah Metode Substitusi. Materi Interpolasi juga dipelajari dalam mata kuliah metode numerik, seperti Interpolasi Linear dan Kuadratik, yang dapat diterapkan dalam situasi sehari-hari.

Terdapat berbagai cara yang dapat digunakan untuk menangani kondisi yang dihadapi dalam pengumpulan data. Namun, jika data yang diperoleh terbatas dan pengambilan data ulang sulit atau mahal dilakukan, maka salah satu opsi yang dapat dilakukan adalah melakukan interpolasi pada data tersebut.

Interpolasi dan ekstrapolasi adalah teknik yang digunakan untuk memprediksi nilai data berdasarkan data yang sudah diketahui. Interpolasi digunakan untuk mencari nilai variabel yang hilang dalam suatu rentang data yang diketahui, sedangkan ekstrapolasi digunakan untuk mencari nilai variabel di luar rentang data yang diketahui. Data yang diperoleh seringkali memiliki pola tertentu, seperti Polinomial atau kelompok. Setiap pola memiliki metode pendekatan yang berbeda, dan penilaian ahli diperlukan untuk menentukan metode yang sesuai berdasarkan riwayat penelitian atau pekerjaan sebelumnya.

A. Pengertian Interpolasi dan Ekstrapolasi

Interpolasi adalah suatu teknik untuk memperkirakan nilai di antara titik-titik data yang telah diketahui. Dalam kehidupan nyata, interpolasi dapat digunakan untuk memperkirakan suatu fungsi yang tidak dapat dijelaskan dengan formula, tetapi hanya berdasarkan data atau tabel, seperti tabel hasil percobaan. Interpolasi dapat digunakan dalam pengolahan citra digital untuk membuat kontur atau dalam proses recovery. Ada beberapa jenis interpolasi yang berbeda berdasarkan fungsinya, seperti interpolasi linier, interpolasi kuadrat, dan interpolasi polinomial. Beberapa metode yang digunakan untuk interpolasi antara lain metode Newton dan Metode Lagrange.

Sebagai contoh, jika terdapat data-data penjualan suatu produk, maka muncul pertanyaan apakah penjualan merupakan fungsi dari waktu. Sebagai contoh, penjualan es campur pada siang hari lebih baik daripada penjualan di malam hari, sehingga penjualan merupakan fungsi dari waktu. Namun, sulit untuk menentukan fungsi yang tepat untuk merepresentasikan data tersebut.

Perbedaan Interpolasi dan Ekstrapolasi

Ekstrapolasi adalah teknik peramalan yang digunakan untuk memproyeksikan kecenderungan masa lalu ke masa depan. Dalam ekstrapolasi, tingkat dan jenis perubahan yang terjadi di masa lalu digunakan untuk memperkirakan perubahan yang akan terjadi di masa depan. Teknik ini digunakan sebagai instrumen perencanaan untuk mengurangi ketidakpastian dalam perencanaan.

Sebagai contoh, jika sebuah organisasi mempekerjakan sejumlah tenaga kerja baru setiap bulan selama dua tahun terakhir, maka dengan menggunakan ekstrapolasi dapat diperkirakan bahwa organisasi tersebut akan mempekerjakan jumlah pekerja yang sama untuk kurun waktu yang sama di masa depan.

B. Rumus dan Metode Interpolasi dan Ekstrapolasi

1. Interpolasi Linier

Interpolasi linier merupakan algoritma matematika yang dapat diterapkan untuk memperkirakan titik median melalui garis lurus pada dua titik entri berurutan. Interpolasi ini adalah polinomial orde pertama dan melintasi garis pada setiap dua titik masuk yang berurutan. Dua titik masuk digunakan untuk memperkirakan interval antara titik data aktual. Metode yang sering digunakan untuk ini adalah interpolasi polinomial.

Kurva untuk Interpolasi Linier

Adapun persamaan dari garis lurus tersebut adalah sebagai berikut :

Untuk menentukan nilai dari interpolasi tersebut, dapat digunakan algoritmatika pengerjaan seperti dibawah ini :

• Tentukan dua titik yang akan dicari penyelesaiannya, dicontohkan sebagai titik  dan .
• Lalu tentukan titik tengah dari kedua titik diatas, contohnya titik X sebagai titik tengahnya.
• Hitung nilai Y dengan rumus diatas.
• Tampilkan nilai titik yang baru.

1. Berikut ini contoh implementasi Interpolasi Linear dengan menggunakan persamaan pada Python :

# Persamaan Interpolasi Linear: y = mx + c
def linear_interpolation(x, x1, y1, x2, y2):
    m = (y2-y1) / (x2-x1)
    c = y1 - m*x1
    return m*x + c
# Contoh penggunaan
x = 3 # Titik yang akan diinterpolasi
x1 = 2 # Titik awal
y1 = 5
x2 = 4 # Titik akhir
y2 = 7
hasil_interpolasi = linear_interpolation(x, x1, y1, x2, y2)
print("Hasil interpolasi pada x={} adalah {}".format(x, hasil_interpolasi))

Hasil Output :

Hasil interpolasi pada x=3 adalah 6

Pada contoh di atas, fungsi linear_interpolation menerima input berupa nilai x yang akan diinterpolasi, serta dua titik x1, y1 dan x2, y2 yang digunakan untuk menghitung kemiringan garis (m) dan konstanta (c) pada persamaan interpolasi linear. Setelah itu, fungsi menghitung dan mengembalikan hasil interpolasi dengan menggunakan persamaan y = mx + c.

Kemudian, pada contoh penggunaan, fungsi linear_interpolation dipanggil dengan parameter yang sesuai. Hasil interpolasi kemudian dicetak pada layar.

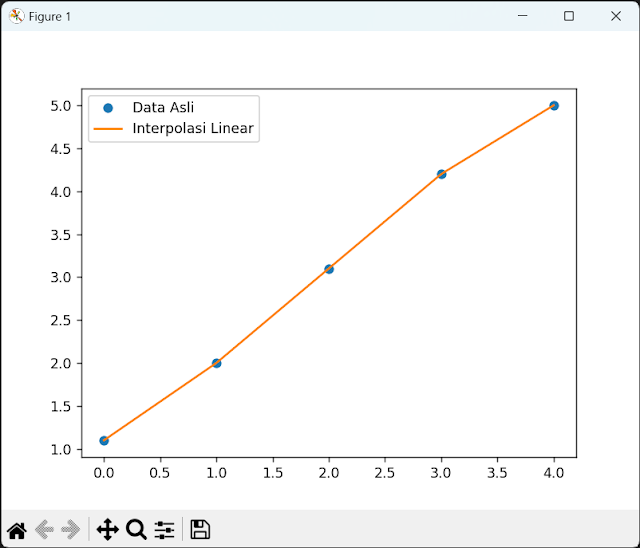
2. Dan inilah contoh Interpolasi Linear menggunakan Library Python :

import numpy as np
import matplotlib.pyplot as plt
# Menyiapkan data
x = np.array([0, 1, 2, 3, 4])
y = np.array([1.1, 2.0, 3.1, 4.2, 5.0])
# Membuat interpolasi linear
def linear_interpolation(x, y, x_interpolate):
    index = np.searchsorted(x, x_interpolate)
    if index == 0:
        return y[0]
    elif index == len(x):
        return y[-1]
    else:
        x0 = x[index-1]
        y0 = y[index-1]
        x1 = x[index]
        y1 = y[index]
        return y0 + (y1 - y0) * (x_interpolate - x0) / (x1 - x0)
# Membuat array untuk hasil interpolasi
x_interpolate = np.linspace(0, 4, 100)
y_interpolate = [linear_interpolation(x, y, xi) for xi in x_interpolate]
# Menampilkan plot
plt.plot(x, y, 'o', label='Data Asli')
plt.plot(x_interpolate, y_interpolate, '-', label='Interpolasi Linear')
plt.legend(loc='best')
plt.show()

Hasil Output :

Penjelasan singkat mengenai kode di atas :

• Pertama-tama, kita menyiapkan data yang akan digunakan untuk melakukan interpolasi linear. Data tersebut adalah x dan y.
• Selanjutnya, kita mendefinisikan sebuah fungsi bernama linear_interpolation, yang akan digunakan untuk melakukan interpolasi linear pada suatu titik x_interpolate.
• Pada fungsi linear_interpolation, kita menggunakan fungsi np.searchsorted untuk mencari indeks dari x yang sesuai dengan x_interpolate. Kemudian, berdasarkan indeks tersebut, kita menghitung nilai interpolasi linearnya.
• Setelah itu, kita membuat sebuah array x_interpolate yang akan digunakan sebagai titik-titik pada sumbu x untuk hasil interpolasi, dan melakukan interpolasi linear pada tiap titik tersebut dengan menggunakan fungsi linear_interpolation.
• Terakhir, kita menampilkan plot hasil interpolasi linear menggunakan matplotlib.

3. Contoh lain dari Interpolasi Linear menggunakan Library Python Matplotlib :

import numpy as np
import matplotlib.pyplot as plt
# Data
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 3, 5, 6, 8])
# Menghitung koefisien m dan c
m, c = np.polyfit(x, y, 1)
# Persamaan garis
eq = f'y = {m:.2f}x + {c:.2f}'
# Plot data asli
plt.scatter(x, y, color='blue', label='Data Asli')
# Plot hasil interpolasi
plt.plot(x, m*x+c, color='red', label=eq)
plt.title('Interpolasi Linear')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()

Hasil Output :

Penjelasan :

• Pertama-tama, kita menyiapkan data berupa array numpy untuk x dan y.
• Selanjutnya, kita menghitung koefisien m (slope) dan c (intercept) menggunakan fungsi polyfit dari NumPy.
• Setelah itu, kita menggunakan koefisien tersebut untuk membentuk persamaan garis yang merepresentasikan hasil interpolasi linear.
• Terakhir, kita membuat plot menggunakan library matplotlib dengan menggunakan scatter untuk data asli dan plot untuk hasil interpolasi linear. Kita juga menambahkan judul, label sumbu, dan legenda pada plot.

2. Interpolasi Kuadratik

Interpolasi Kuadratik sebenarnya hampir sama dengan interpolasi linier, namun interpolasi ini menggunakan kekuatan 3 titik untuk membentuk garis. Banyak aplikasi interpolasi linier tidak maksimal saat menggunakan fungsi pangkat dua, jadi interpolasi kuadrat ada untuk menyelesaikan fungsi pangkat dua dan menemukan titik baru secara efisien. 

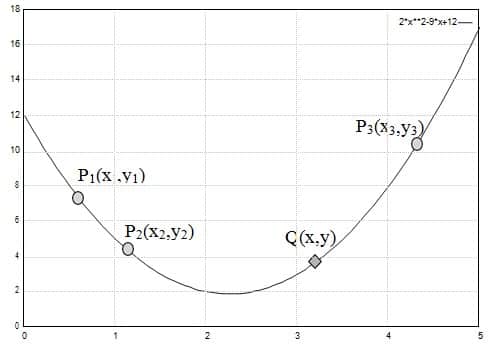Kurva untuk Interpolasi Kuadratik

Dari gambar diatas terlihat bahwa pada interpolasi ini digunakan tiga titik, yaitu :

, , dan 

Sedangkan nilai Q sendiri merupakan rata-rata dari suatu titik yang ada, namun dapat dicari dengan menggunakan rumus berikut untuk mencari titik Q(x, y) :

Adapun untuk mengerjakan soal-soal yang berkaitan dengan interpolasi kuadratik dapat dikerjakan dengan menggunakan algoritma pengerjaan sebagai beikut :

• Tentukan tiga titik yang akan dicari penyelesaiannya, dicontohkan sebagai titik , , dan .
• Lalu tentukan titik tengah dari kedua titik diatas, contohnya titik P4(x,y) sebagai titik tengahnya.
• Hitung nilai Y dengan rumus diatas.
• Tampilkan nilai titik yang baru.

1. Berikut adalah contoh Interpolasi Kuadratik dengan menggunakan Python dan persamaan :

import numpy as np
# Fungsi untuk menghitung koefisien dalam persamaan kuadratik
def quadratic_coeffs(x1, y1, x2, y2, x3, y3):
    denom = (x1 - x2) * (x1 - x3) * (x2 - x3)
    A = (x3 * (y2 - y1) + x2 * (y1 - y3) + x1 * (y3 - y2)) / denom
    B = (x3**2 * (y1 - y2) + x2**2 * (y3 - y1) + x1**2 * (y2 - y3)) / denom
    C = (x2 * x3 * (x2 - x3) * y1 + x3 * x1 * (x3 - x1) * y2 + x1 * x2 * (x1 - x2) * y3) / denom
    return A, B, C
# Data titik-titik yang diketahui
x = [0, 1, 2]
y = [1, 2, 3]
# Hitung koefisien dalam persamaan kuadratik
A, B, C = quadratic_coeffs(x[0], y[0], x[1], y[1], x[2], y[2])
# Buat array nilai x yang akan dihitung nilainya
x_new = np.linspace(0, 2, 100)
# Hitung nilai y yang sesuai menggunakan persamaan kuadratik
y_new = A * x_new**2 + B * x_new + C
# Print hasil
print(y_new)

Output :

[1.         1.02020202 1.04040404 1.06060606 1.08080808 1.1010101
 1.12121212 1.14141414 1.16161616 1.18181818 1.2020202  1.22222222
 1.24242424 1.26262626 1.28282828 1.3030303  1.32323232 1.34343434
 1.36363636 1.38383838 1.4040404  1.42424242 1.44444444 1.46464646
 1.48484848 1.50505051 1.52525253 1.54545455 1.56565657 1.58585859
 1.60606061 1.62626263 1.64646465 1.66666667 1.68686869 1.70707071
 1.72727273 1.74747475 1.76767677 1.78787879 1.80808081 1.82828283
 1.84848485 1.86868687 1.88888889 1.90909091 1.92929293 1.94949495
 1.96969697 1.98989899 2.01010101 2.03030303 2.05050505 2.07070707
 2.09090909 2.11111111 2.13131313 2.15151515 2.17171717 2.19191919
 2.21212121 2.23232323 2.25252525 2.27272727 2.29292929 2.31313131
 2.33333333 2.35353535 2.37373737 2.39393939 2.41414141 2.43434343
 2.45454545 2.47474747 2.49494949 2.51515152 2.53535354 2.55555556
 2.57575758 2.5959596  2.61616162 2.63636364 2.65656566 2.67676768
 2.6969697  2.71717172 2.73737374 2.75757576 2.77777778 2.7979798
 2.81818182 2.83838384 2.85858586 2.87878788 2.8989899  2.91919192
 2.93939394 2.95959596 2.97979798 3.        ]

Berikut adalah penjelasan mengenai setiap bagian kode program tersebut:

• def quadratic_coeffs(x1, y1, x2, y2, x3, y3) : Fungsi yang digunakan untuk menghitung koefisien dalam persamaan kuadratik. Menerima enam argumen yang merupakan koordinat tiga titik yang diketahui (x1, y1), (x2, y2), dan (x3, y3). Mengembalikan nilai koefisien A, B, dan C.
• x = [0, 1, 2] dan y = [1, 2, 3] : Data titik-titik yang diketahui.
• A, B, C = quadratic_coeffs(x[0], y[0], x[1], y[1], x[2], y[2]) : Memanggil fungsi quadratic_coeffs untuk menghitung koefisien A, B, dan C dalam persamaan kuadratik berdasarkan titik-titik yang diketahui.
• x_new = np.linspace(0, 2, 100) : Membuat array x_new yang berisi 100 nilai yang merata terdistribusi antara 0 dan 2.

2. Berikut ini adalah contoh implementasi interpolasi kuadratik dengan menggunakan persamaan dan visualisasi menggunakan library Matplotlib pada Python :

import numpy as np
import matplotlib.pyplot as plt
# Input data
x = np.array([-2, -1, 0, 1, 2])
y = np.array([3, 1, -1, 1, 3])
# Matriks koefisien
A = np.vstack([np.ones(3), x[:3], x[:3]**2]).T
# Matriks solusi
b = y[:3]
# Mencari solusi persamaan
coeff = np.linalg.solve(A, b)
# Interpolasi kuadratik
x_new = np.linspace(-2, 2, num=100)
y_new = coeff[0] + coeff[1]*x_new + coeff[2]*x_new**2
# Visualisasi hasil interpolasi
plt.plot(x_new, y_new, label='Interpolasi')
plt.scatter(x, y, label='Data Asli')
plt.legend()
plt.show()

Hasil Output :

Penjelasan singkat dari program di atas adalah sebagai berikut:

• Pertama-tama, kita memasukkan data x dan y yang akan diinterpolasi.
• Selanjutnya, kita membuat matriks koefisien A dan matriks solusi b untuk persamaan kuadratik y = a + bx + cx^2 dengan menggunakan data x dan y yang tersedia.
• Kemudian, kita mencari solusi dari persamaan tersebut dengan menggunakan fungsi np.linalg.solve.
• Setelah itu, kita membuat data x_new yang merupakan himpunan titik-titik pada rentang x yang baru, dan menghitung nilai y_new dengan menggunakan koefisien yang telah ditemukan sebelumnya.
• Akhirnya, kita visualisasikan hasil interpolasi kuadratik tersebut dengan menggunakan fungsi plt.plot dan plt.scatter.

Output dari program di atas adalah sebuah gambar yang menunjukkan hasil interpolasi kuadratik dari data yang diberikan.

3 Interpolasi Polinomial

Interpolasi polynomial digunakan untuk mencari titik-titik antara dari n buah titik , , , …,  dengan menggunakan pendekatan fungsi polynomial pangkat n-1 :

Masukkan nilai dari setiap titik ke dalam persamaan polynomial di atas dan diperoleh persamaan simultan dengan n persamaan dan n variable bebas :

Adapun algoritma untuk mengerjakan soal-soal dari Interpolasi Polinom adalah sebagai berikut :

• Menentukan jumlah titik N yang diketahui.
• Memasukkan titik-titik yang diketahui Pi = (x_i, y_i) untuk i = 1,2,3,…..,N.

Menyusun augment matriks dari titik-titik yang diketahui sebagai berikut :

• Menyelesaikan persamaan simultan dengan augment matriks diatas dengan menggunakan Metode Eliminasi Gauss/Jordan.
• Menyusun koefisien fungsi polynomial berdasarkan penyelesaian persamaan simultan dia atas.

• Memasukkan nilai x dari titik yang diketahui.
• Menghitung nilai y dari fungsi polynomial yang dihasilkan

• Menghasilkan nilai (x, y)

4. Interpolasi Lagrange

Interpolasi Lagrange adalah salah satu formula untuk interpolasi berselang tidak sama selain formula interpolasi Newton umum & Metode Aitken. Walaupun demikian dapat digunakan pula untuk interpolasi berselang sama.

Misalkan fungsi y (x) kontinu & diferensiabel sampai turunan (n+1) dalam interval buka (a, b). Diberikan (n+1) titik (x₀, y₀), (x₁, y₁), …, (x_n, y_n) dengan nilai x tidak perlu berjarak sama dengan yang lainnya, dan akan dicari suatu polinom berderajat n. Untuk pemakaian praktis, formula interpolasi Lagrange dapat dinyatakan sebagai berikut :

Algoritma Interpolasi Lagrange :

• Tentukan jumlah titik (N) yang diketahui
• Tentukan titik-titik Pi(x_i, y_i) yang diketahui dengan i=1,2,3,…,N
• Tentukan x dari titik yang dicari
• Hitung nilai y dari titik yang dicari dengan formulasi Interpolasi Lagrange
• Tampilkan nilai (x,y)

Untuk melihat dan mempelajari Interpolasi dan Ekstrapolasi dengan menggunakan Microsoft Excel, silakan lihat di sini (Bsuite365.com) dan di sini (Broexcel.com).

VIDEO

Untuk memahami lebih lanjut terkait dengan Interpolasi dan Ekstrapolasi dalam Curve Fitting, lihatlah Video-video YouTube di bawah ini.

Semoga bermanfaat bagi semua Mahasiswa Teknik yang mengambil Mata Kuliah Metode Numerik.

Terima Kasih 😄😘👌👍 :)

Wassalamu‘alaikum wr. wb.