Assalamu‘alaikum wr. wb.
Hello guys! Dalam Komputer, kita hanya mengenal Sistem Bilangan seperti Bilangan Biner merupakan Sistem Bilangan berbasis 2, Bilangan Oktal merupakan Sistem Bilangan berbasis 8, dan juga Bilangan Heksadesimal merupakan Sistem Bilangan berbasis 16. Dan Jenis Sistem Bilangan yang biasa kita pakai dan dapat dipahami oleh Manusia adalah Bilangan Desimal.
Kali ini kita akan membahas tentang Jenis-jenis Sistem Bilangan (Numeral Systems) yang dipakai dalam Komputer dan Peradaban Dunia.
Artikel Utama : Wikipedia.org (Radix) dan Wikipedia.org (List of Numeral Systems)
PENGERTIAN
Dalam sistem Angka Posisional, radix atau basis adalah jumlah digit unik, termasuk angka nol, yang digunakan untuk mewakili angka. Misalnya, untuk sistem desimal/denary (sistem yang paling umum digunakan saat ini) radix (bilangan dasar) adalah sepuluh, karena menggunakan sepuluh digit dari 0 hingga 9.
Dalam sistem penomoran posisi standar manapun, suatu bilangan biasanya ditulis sebagai (x)y dengan x sebagai deretan angka dan y sebagai basisnya, meskipun untuk basis sepuluh subskrip biasanya diasumsikan (dan dihilangkan, bersama dengan pasangan tanda kurung) , karena ini adalah cara paling umum untuk mengekspresikan nilai. Misalnya, (100)10 setara dengan 100 (Sistem Desimal tersirat dalam yang terakhir) dan mewakili angka Seratus, sedangkan (100)2 (dalam sistem biner dengan basis 2 mewakili angka Empat.
Dalam Sistem Bilangan
Dalam Sistem dengan Radix (Basis) 13, misalnya, Rangkaian Angka seperti 398 menunjukkan angka (desimal) 3 × 132 + 9 × 131 + 8 × 130 = 632.
Lebih umum, dalam sistem dengan radix b (b > 1), deretan angka d1 … dn menunjukkan bilangan d1bn−1 + d2bn−2 + … + dnb0, di mana 0 ≤ di < b. Berbeda dengan desimal, atau Radix 10, yang memiliki tempat satu, tempat puluhan, tempat ratusan, dan seterusnya, radix b akan memiliki tempat satuan, kemudian tempat b1, tempat b2, dll.
Sistem Bilangan yang umum digunakan antara lain :
Base/Radix | Nama | Deskripsi |
2 | Sistem Bilangan Biner | Digunakan secara internal oleh hampir semua komputer, adalah basis 2. Dua digit adalah "0" dan "1", dinyatakan dari sakelar yang menampilkan OFF dan ON, masing-masing. Digunakan di sebagian besar penghitung listrik. |
8 | Sistem Bilangan Oktal | Digunakan sesekali dalam komputasi. Delapan digit adalah "0"–"7" dan mewakili 3 bit (23). |
10 | Sistem Bilangan Desimal | Sistem Bilangan yang paling banyak digunakan di dunia, digunakan dalam Aritmatika. Sepuluh digitnya adalah "0"–"9". Digunakan di sebagian besar penghitung mekanis. |
12 | Sistem Duodesimal (Dozenal) | Kadang-kadang dianjurkan karena dapat dibagi dengan 2, 3, 4, dan 6. Secara tradisional digunakan sebagai bagian dari jumlah yang dinyatakan dalam puluhan dan Bruto. |
16 | Sistem Heksadesimal | Sering digunakan dalam Komputasi sebagai representasi biner yang lebih kompak (1 digit hex per 4 bit). Enam belas digit adalah "0"–"9" diikuti oleh "A"–"F" atau "a"–"f". |
20 | Sistem Vigesimal | Sistem angka tradisional di beberapa budaya, masih digunakan oleh beberapa orang untuk berhitung. Secara historis juga dikenal sebagai sistem skor dalam bahasa Inggris, sekarang paling terkenal dalam frasa "empat skor dan tujuh tahun lalu" di Alamat Gettysburg. |
60 | Sistem Seksagesimal | Berasal dari Sumeria kuno dan diteruskan ke Babilonia. Digunakan saat ini sebagai dasar sistem koordinat melingkar modern (derajat, menit, dan detik) dan pengukuran waktu (menit, dan detik) dengan analogi rotasi Bumi. |
Sistem Oktal dan heksadesimal sering digunakan dalam komputasi karena kemudahannya sebagai singkatan untuk biner. Setiap Digit Heksadesimal sesuai dengan urutan Empat Digit biner, karena 16 (Enam Belas) adalah pangkat empat dari dua; misalnya, Heksadesimal 7816 adalah Biner 11110002. Demikian pula, setiap digit oktal sesuai dengan urutan unik dari tiga digit biner, karena delapan adalah pangkat tiga dari dua.
Representasi ini unik. Misalkan b adalah bilangan bulat positif yang lebih besar dari 1. Maka setiap bilangan bulat positif a dapat dinyatakan secara unik dalam bentuk :
Di mana m adalah bilangan bulat nonnegatif dan r adalah bilangan bulat sehingga :
0 < rm < b dan 0 ≤ ri < b untuk i = 0, 1, ... , m − 1
Radikal biasanya bilangan asli. Namun, sistem posisi lain dimungkinkan, misalnya, basis rasio emas (yang radixnya adalah bilangan aljabar non-bilangan bulat), dan basis negatif (yang radix-nya negatif). Basis negatif memungkinkan representasi bilangan negatif tanpa menggunakan tanda minus. Misalnya, misalkan b = 10. Kemudian serangkaian angka seperti 19 menunjukkan Angka (Desimal) 1 × (−10)1 + 9 × (−10)0 = −1.
DAFTAR SISTEM BILANGAN
A. Menurut Budaya / Periode Waktu
Nama | Basis | Sampel | Perkiraan Penampilan Pertama |
10+60 | 3.100 SM | ||
10 | 3.000 SM | ||
10+60 | 2.000 SM | ||
| Korean numerals (Sino-Korean) Vietnamese numerals (Sino-Vietnamese) | 10 | 零一二三四五六七八九十百千萬億 (Default, Traditional Chinese) 〇一二三四五六七八九十百千万亿 (Default, Simplified Chinese) 零壹貳參肆伍陸柒捌玖拾佰仟萬億 (Financial, T. Chinese) 零壹贰叁肆伍陆柒捌玖拾佰仟萬億 (Financial, S. Chinese) | 1.600 SM |
10 | 1.500 SM | ||
10 | ০ ১ ২ ৩ ৪ ৫ ৬ ৭ ৮ ৯ | 1.400 SM | |
I V X L C D M | 1,000 SM | ||
10 | א ב ג ד ה ו ז ח ט י כ ל מ נ ס ע פ צ ק ר ש ת ך ם ן ף ץ | 800 SM | |
10 | Tamil ௧ ௨ ௩ ௪ ௫ ௬ ௭ ௮ ௯ ௰ Devanagari ० १ २ ३ ४ ५ ६ ७ ८ ९ Tibetan ༠ ༡ ༢ ༣ ༤ ༥ ༦ ༧ ༨ ༩ | 750 – 690 SM | |
10 | ō α β γ δ ε ϝ ζ η θ ι ο Αʹ Βʹ Γʹ Δʹ Εʹ Ϛʹ Ζʹ Ηʹ Θʹ | <400 SM | |
10 | 𐤙 𐤘 𐤗 𐤛𐤛𐤛 𐤛𐤛𐤚 𐤛𐤛𐤖 𐤛𐤛 𐤛𐤚 𐤛𐤖 𐤛 𐤚 𐤖 [1] | <250 SM | |
Chinese rod numerals | 10 | 𝍠 𝍡 𝍢 𝍣 𝍤 𝍥 𝍦 𝍧 𝍨 𝍩 | Abad ke-1 |
10 | ፩ ፪ ፫ ፬ ፭ ፮ ፯ ፰ ፱ ፲ ፳ ፴ ፵ ፶ ፷ ፸ ፹ ፺ ፻ | Abad ke-3 – ke-4 Abad ke-15 (Gaya Modern) | |
10 | Ա Բ Գ Դ Ե Զ Է Ը Թ Ժ | Awal Abad ke-5 | |
10 | ០ ១ ២ ៣ ៤ ៥ ៦ ៧ ៨ ៩ | Awal Abad ke-7 | |
10 | ๐ ๑ ๒ ๓ ๔ ๕ ๖ ๗ ๘ ๙ | Abad ke-7 | |
10 | غ ظ ض ذ خ ث ت ش ر ق ص ف ع س ن م ل ك ي ط ح ز و هـ د ج ب ا | < Abad ke-8 | |
10 | ٩ ٨ ٧ ٦ ٥ ٤ ٣ ٢ ١ ٠ | Abad ke-8 | |
10 | 𠬠 𠄩 𠀧 𦊚 𠄼 𦒹 𦉱 𠔭 𠃩 | < Abad ke-9 | |
10 | 0 1 2 3 4 5 6 7 8 9 | Abad ke-9 | |
10 | Ⰰ Ⰱ Ⰲ Ⰳ Ⰴ Ⰵ Ⰶ Ⰷ Ⰸ ... | Abad ke-9 | |
10 | а в г д е ѕ з и ѳ і ... | Abad ke-10 | |
10 | Abad ke-10 | ||
10 | ၀ ၁ ၂ ၃ ၄ ၅ ၆ ၇ ၈ ၉ | Abad ke-11 | |
10 | 𘈩 𗍫 𘕕 𗥃 𗏁 𗤁 𗒹 𘉋 𗢭 𗰗 | Abad ke-11 (1036 M) | |
10 | Abad ke-13 | ||
5+20 | < Abad ke-15 | ||
20 | < Abad ke-15 | ||
10 | 하나 둘 셋 넷 다섯 여섯 일곱 여덟 아홉 열 | Abad ke-15 (1443 M) | |
20 | Abad ke-16 | ||
10 | ෦ ෧ ෨ ෩ ෪ ෫ ෬ ෭ ෮ ෯ 𑇡 𑇢 𑇣 𑇤 𑇥 𑇦 𑇧 𑇨 𑇩 𑇪 𑇫 𑇬 𑇭 𑇮 𑇯 𑇰 𑇱 𑇲 𑇳 𑇴 | < Abad ke-18 | |
10 | Abad ke-19 | ||
10 | Abad ke-19 (1820-an) | ||
5+20 | Abad ke-20 (1994) |
B. Menurut Jenis Notasi
1. Sistem Bilangan Posisi Standar
Sistem bilangan diklasifikasikan di sini apakah mereka menggunakan notasi posisi (juga dikenal sebagai notasi nilai tempat), dan selanjutnya dikategorikan berdasarkan radix atau basis.
Biner/Binary (Basis 2)
Komputasi digital, volume imperial dan biasa (bushel-kenning-peck-gallon-pottle-quart-pint-cup-gill-jack-fluid ons-sendok makan).
Terner/Ternary (Basis 3)
Himpunan Cantor (semua titik dalam [0,1] yang dapat direpresentasikan dalam ternary tanpa 1s); menghitung Tasbih dalam Islam; sistem pengukuran hand-foot-yard dan sendok teh-sendok-sendok; basis bilangan bulat paling ekonomis.
Kuarterner/Quaternary (Basis 4)
Transmisi data, Basis DNA dan kurva Hilbert; Bahasa Chumashan, dan angka Kharosthi
Kuiner/Quinary (Basis 5)
Bahasa Gumatj, Ateso, Nunggubuyu, Kuurn Kopan Noot, dan Saraveca; pengelompokan hitungan umum mis. tanda penghitungan.
Sener/Senary (Base 6)
Diceware (Dadu), Bahasa Ndom, Kanum, dan Bahasa Proto-Uralic (dicurigai).
Septener/Septenary (Basis 7)
Ketepatan waktu Pekan, notasi huruf musik Barat.
Oktal/Octal (Basis 8)
Charles XII dari Swedia, izin mirip Unix, kode Squawk, DEC PDP-11, notasi ringkas untuk bilangan biner, Xiantian (I Ching, Tiongkok).
Noner/Nonary (Basis 9)
Pengkodean Basis 9; notasi kompak untuk Terner.
Desimal/Decimal/Denary (Basis 10)
Paling banyak digunakan oleh peradaban modern.
Undesimal/Undecimal (Basis 11)
Sistem bilangan basis-11 dikaitkan dengan suku Māori (Selandia Baru) pada abad ke-19 dan Pangwa (Tanzania) pada abad ke-20. Diusulkan secara singkat selama Revolusi Prancis untuk menyelesaikan perselisihan antara mereka yang mengusulkan pergeseran ke duodesimal dan mereka yang puas dengan desimal. Digunakan sebagai cek digit dalam ISBN untuk 10 digit ISBN.
Duodesimal/Duodecimal (Basis 12)
Bahasa di Nigerian Middle Belt Janji, Gbiri-Niragu, Piti, dan dialek Nimbia dari Gwandara; bahasa Chepang di Nepal, dan dialek Mahl di Maladewa; penghitungan kotor selusin-kotor-besar; Ketepatan waktu 12 jam dan bulan; Tahun Zodiak Tiongkok; kaki dan inci; pecahan Romawi; sen dan shilling.
Tridesimal/Tridecimal (Basis 13)
Pengkodean Basis 13; Fungsi dasar Conway 13.
Tetradesimal/Tetradecimal (Basis 14)
Pemrograman untuk Kalkulator HP 9100A/B dan aplikasi pemrosesan gambar; pound dan batu.
Pentadesimal/Pentadecimal (Basis 15)
Perutean telepon melalui IP, dan bahasa Huli.
Heksadesimal/Hexadecimal atau Seksadesimal/Sexadecimal (Basis 16)
Pengkodean Basis 16; notasi ringkas untuk data biner; sistem nada; ons dan pon.
Heptadesimal/Heptadecimal (Basis 17)
Pengkodean Basis 17.
Oktodesimal/Octodecimal (Basis 18)
Pengkodean Basis18; Basis sedemikian rupa sehingga 7n palindromik untuk n = 3, 4, 6, 9.
Enneadesimal/Enneadecimal (Basis 19)
Pengkodean Basis 19.
Vigesimal (Basis 20)
Angka Basque, Celtic, Maya, Muisca, Inuit, Yoruba, Tlingit, dan Dzongkha; Santali, dan bahasa Ainu; shilling dan pound
Pengkodean Base21; juga basis terkecil di mana semua 1/2 sampai 1/18 memiliki periode 4 atau lebih pendek.
Duovigesimal (Basis 22)
Pengkodean Basis 22.
Trivigesimal (Basis 23)
Bahasa Kalam dan Bahasa Kobon yang ada di Papua Nugini.
Tetravigesimal (Basis 24)
Ketepatan waktu 24 Jam; bahasa Kaugel.
Pentavigesimal (Basis 25)
Notasi ringkas untuk Quinary.
Heksavigesimal/Hexavigesimal (Basis 26)
Pengkodean Basis 26, terkadang digunakan untuk enkripsi atau penyandian, menggunakan semua huruf dalam alfabet bahasa Inggris.
Heptavigesimal/Septemvigesimal (Basis 27)
Bahasa Telefol dan Oksapmin. Pemetaan angka bukan nol ke alfabet dan nol ke spasi kadang-kadang digunakan untuk menyediakan checksum untuk data alfabet seperti nama pribadi, untuk memberikan pengkodean singkat string alfabet, atau sebagai dasar untuk bentuk gematria. Notasi ringkas untuk ternary.
Oktovigesimal/Octovigesimal (Basis 28)
Pengkodean Basis 28, bulan ketepatan waktu.
Enneavigesimal (Basis 29)
Pengkodean Basis 29.
Kode Area Alam, ini adalah basis terkecil sehingga semua
1/2 sampai 1/6 berakhir, suatu bilangan n adalah bilangan biasa jika dan hanya jika 1/n berakhir pada basis 30.
Untrigesimal (Basis 31)
Pengkodean Basis 31.
Duotrigesimal (Basis 32)
Pengkodean Basis 32, dan Bahasa Ngiti (Bahasa di Kongo, Afrika).
Tritrigesimal (Basis 33)
Penggunaan huruf (kecuali I, O, Q) dengan angka di plat nomor kendaraan Hong Kong.
Tetratrigesimal (Basis 34)
Menggunakan semua angka dan semua huruf kecuali I dan O; basis terkecil di mana 1/2 berakhir dan semua 1/2 hingga 1/18 memiliki periode 4 atau lebih pendek.
Pentatrigesimal (Basis 35)
Menggunakan semua angka dan semua huruf kecuali O.
Heksatrigesimal/Hexatrigesimal (Basis 36)
Pengkodean Basis 36, penggunaan huruf dengan angka.
Heptatrigesimal (Basis 37)
Pengkodean Basis 37; menggunakan semua angka dan semua huruf alfabet Spanyol.
Oktotrigesima/Octotrigesimal (Basis 38)
Pengkodean Basis 38; gunakan semua digit Duodesimal dan semua huruf.
Enneatrigesimal (Basis 39)
Pengkodean Basis 39.
Kuadragesimal/Quadragesimal (Basis 40)
Pengkodean DEC RADIX 50/MOD40 digunakan untuk merepresentasikan nama file dan simbol lainnya secara ringkas pada komputer Digital Equipment Corporation. Himpunan karakter adalah bagian dari ASCII yang terdiri dari spasi, huruf besar, tanda baca "$", ".", dan "%", dan angka.
Duokuadragesimal/Duoquadragesimal (Basis 42)
Pengkodean Basis 42; basis terbesar yang semua bilangan prima minimalnya diketahui.
Pentakuadragesimal/Pentaquadragesimal (Basis 45)
Pengkodean Basis 45.
Septakuadragesimal/Septaquadragesimal (Basis 47)
Basis terkecil yang tidak diketahui bilangan prima Wieferich umum.
Oktokuadragesimal/Octoquadragesimal (Basis 48)
Pengkodean Basis 48.
Enneakuadragesimal/Enneaquadragesimal (Basis 49)
Notasi ringkas untuk Septener (Basis 7).
Kuinkuagesimal/Quinquagesimal (Basis 50)
Pengkodean Basis 50; Encoding SQUOZE digunakan untuk merepresentasikan nama file dan simbol lainnya secara ringkas pada beberapa komputer IBM. Encoding menggunakan semua karakter Gurmukhi ditambah angka Gurmukhi.
Duokuinkuagesimal/Duoquinquagesimal (Basis 52)
Pengkodean Basis 52, varian Base62 tanpa vokal kecuali Y dan y atau varian Basis 26 menggunakan semua huruf kecil dan besar.
Tetrakuinkuagesimal/Tetraquinquagesimal (Basis 54)
Pengkodean Basis 54.
Heksakuinkuagesimal/Hexaquinquagesimal (Basis 56)
Pengkodean Basis 56, varian dari Basis 58.
Heptakuinkuagesimal/Heptaquinquagesimal (Basis 57)
Pengkodean Basis 57, varian dari Basis 62 tidak termasuk I, O, l, U, dan u atau I, 1, l, 0, dan O.
Oktokuinkuagesimal/Octoquinquagesimal (Basis 58)
Pengkodean Basis 58, varian Basis 62 tidak termasuk 0 (nol), I (kapital i), O (kapital o) dan l (huruf kecil L).
Seksagesimal/Sexagesimal (Basis 60)
Angka Babilonia, NewBase60 Encoding, mirip dengan Basis 62, tidak termasuk I, O, dan l, tetapi termasuk _(garis bawah); sistem pengukuran derajat-menit-detik dan jam-menit-detik; Ekari dan Bahasa Sumeria.
Duoseksagesimal/Duosexagesimal (Basis 62)
Pengkodean Basis 62, menggunakan 0–9, A–Z, dan a–z.
Tetraseksagesimal/Tetrasexagesimal (Basis 64)
Pengkodean Basis 64; I Ching di Tiongkok. Sistem ini dengan mudah dikodekan ke dalam ASCII dengan menggunakan 26 huruf alfabet Latin dalam huruf besar dan kecil (total 52) ditambah 10 angka (total 62) dan kemudian menambahkan dua karakter khusus (+ dan /).
Septuagesimal (Basis 70)
Pengkodean Basis 70.
Duoseptuagesimal (Basis 72)
Pengkodean Basis 72; basis terkecil >2 sehingga tidak ada Bilangan Narsis 3 digit.
Oktogesimal/Octogesimal (Basis 80)
Pengkodean Basis 80.
Unoktogesimal/Unoctogesimal (Basis 81)
Pengkodean Basis 81, menggunakan as 81 = 34 terkait dengan Ternary.
Pentoktogesimal/Pentoctogesimal (Basis 85)
Pengkodean Ascii85. Ini adalah jumlah minimum karakter yang diperlukan untuk mengkodekan angka 32 bit menjadi 5 karakter yang dapat dicetak dalam proses yang mirip dengan pengkodean MIME-64, karena 855 hanya sedikit lebih besar dari 232. Metode tersebut 6,7% lebih efisien daripada MIME-64 yang mengkodekan nomor 24 bit menjadi 4 karakter yang dapat dicetak.
Enneaoktogesimal/Enneaoctogesimal (Basis 89)
Basis terbesar yang diketahui semua bilangan prima yang dapat dipotong kiri.
Nonagesimal (Basis 90)
Terkait dengan dugaan Goormaghtigh untuk nomor repunit umum (111 di basis 90 = 11111111111111 di basis 2).
Unnonagesimal (Basis 91)
Pengkodean Basis 91, menggunakan semua ASCII kecuali "-" (0x2D), "\" (0x5C), dan "'" (0x27); satu varian menggunakan "\" (0x5C) sebagai ganti """ (0x22).
Duononagesimal (Basis 92)
Pengkodean Basis 92, menggunakan semua ASCII kecuali untuk "`" (0x60) dan """ (0x22) karena membingungkan.
Trinonagesimal (Basis 93)
Pengkodean Basis 93, menggunakan semua karakter ASCII yang dapat dicetak kecuali untuk "," (0x27) dan "-" (0x3D) serta karakter Spasi. "," dicadangkan untuk pembatas dan "-" dicadangkan untuk negasi.
Tetranonagesimal (Basis 94)
Pengkodean Basis 94, menggunakan semua karakter ASCII yang dapat dicetak.
Pentanonagesimal (Basis 95)
Pengkodean Basis 95, varian Basis 94 dengan penambahan karakter Spasi.
Heksanonagesimal/Hexanonagesimal (Basis 96)
Pengkodean Basis 96, menggunakan semua karakter ASCII yang dapat dicetak serta dua digit duodesimal tambahan.
Septanonagesimal (Basis 97)
Basis terkecil yang bukan pangkat ganjil sempurna (di mana bilangan Wagstaff yang digeneralisasi dapat difaktorkan secara Aljabar) yang tidak diketahui bilangan prima Wagstaff-nya.
Sentesimal/Centesimal (Basis 100)
Sebagai 100=102, ini adalah dua angka Desimal.
Sentevigesimal/Centevigesimal (Basis 120)
Pengkodean Basis 120.
Senteunvigesimal/Centeunvigesimal (Basis 121)
Terkait dengan Basis 11 (Undesimal).
Sentepentavigesimal/Centepentavigesimal (Basis 125)
Terkait dengan Basis 5 (Kuiner/Quinary).
Senteoktovigesimal/Centeoctovigesimal (Basis 128)
Menggunakan sebagai 128=27.
Sentetetrakuadragesimal/Centetetraquadragesimal (Basis 144)
Dua digit Duodesimal.
Sentenovemseksagesimal/Centenovemsexagesimal (Basis 169)
Dua digit Tridesimal.
Sentepentoktogesimal/Centepentoctogesimal (Basis 185)
Basis terkecil yang bukan pangkat sempurna (di mana repunit umum dapat difaktorkan secara aljabar) yang tidak diketahui bilangan prima repunit umum.
Senteheksanonagesimal/Centehexanonagesimal (Basis 196)
Dua digit Tetradesimal.
Duosentesimal/Duocentesimal (Basis 200)
Pengkodean Basis 200.
Duosentedesimal/Duocentedecimal (Basis 210)
Basis terkecil sehingga semua 1/2 hingga 1/10 berakhir.
Duosenteheksidesimal/Duocentehexidecimal (Basis 216)
Berhubungan dengan Basis 6.
Duosentepentavigesimal/Duocentepentavigesimal (Basis 225)
Dua digit Pentadesimal.
Duosenteheksakuinkuagesimal/Duocentehexaquinquagesimal (Basis 256)
Pengkodean Basis 256, sebagai 256=28.
Tresentesimal/Trecentesimal (Basis 300)
Pengkodean Basis 300.
Tresentoseksagesimal/Trecentosexagesimal (Basis 360)
2. Bilangan Basis Negatif
Nama-nama umum dari Sistem Bilangan dasar Negatif dibentuk menggunakan awalan nega-, memberikan nama-nama seperti :
Basis | Nama |
| −2 | Negabinary Negabiner |
| −3 | Negaternary Negaterner |
| −4 | Negaquaternary Negakuarterner |
| −5 | Negaquinary Negakuiner |
| −6 | Negasenary Negasener |
| −8 | Negaoctal Negaoktal |
| −10 | Negadecimal Negadesimal |
| −12 | Negaduodecimal Negaduodesimal |
| −16 | Negahexadecimal Negaheksadesimal |
3. Bilangan Basis Kompleks
Basis | Nama | Kegunaan |
2i | Quater-imaginary base | Terkait dengan Basis 4 dan Basis 16 |
| Base | Terkait dengan Basis -2 dan Basis 4 | |
| Base | Terkait dengan Basis 2 | |
| 2ω | Base 2ω | Terkait dengan Basis 8 |
| Base | Terkait dengan Basis 2 | |
−1 ± i | Twindragon base | Bentuk Fraktal Twindragon, terkait dengan Basis 4 dan Basis 16 |
1 ± i | Nega-Twindragon base | Terkait dengan Basis -4 dan Basis 16 |
4. Bilangan Basis Non-Bilangan Bulat
- Basis
: Basis non-Bilangan Bulat Rasional
- Basis
: Terkait dengan Duodesimal
- Basis
: Terkait dengan Desimal
- Basis
: Terkait dengan Basis 2 (Biner)
- Basis
: Terkait dengan Basis 3 (Terner)
- Basis
- Basis
- Basis
: Penggunaan dalam sistem musik temperamen 12 nada yang sama
- Basis
- Basis
: Basis non-bilangan bulat rasional negatif
- Basis
: A negative non-integer base, related to base 2
- Basis
: Terkait dengan Desimal
- Basis
: Terkait dengan Duodesimal
- Basis φ (Basis Rasio Emas / Golden Ratio Base) : Encoder Beta awal
- Basis ρ (Basis Bilangan Plastik / Plastic Number Base)
- Basis ψ (Basis Rasio Supergolden / Supergolden Ratio Base)
- Basis
- Basis e : Ekonomi Radiks terendah
- Basis π
- Basis eπ
- Basis
5. Radiks Campuran
- Factorial number system {1, 2, 3, 4, 5, 6, ...}
- Even double factorial number system {2, 4, 6, 8, 10, 12, ...}
- Odd double factorial number system {1, 3, 5, 7, 9, 11, ...}
- Primorial number system {2, 3, 5, 7, 11, 13, ...}
- Fibonorial number system {1, 2, 3, 5, 8, 13, ...}
- {60, 60, 24, 7} in timekeeping
- {60, 60, 24, 30 (or 31 or 28 or 29), 12, 10, 10, 10} in timekeeping
- (12, 20) traditional English monetary system (£sd)
- (20, 18, 13) Maya timekeeping
JENIS-JENIS SISTEM BILANGAN
1. Bilangan Biner (Basis 2)
Sumber Artikel : Wikipedia.org, Monitorteknologi.com, Teknikelektro.com, Teknikelektronika.com, dan CS.Utexas.edu (PDF) (Sebagian)
Bahasa Mesin adalah Biner. Ini berarti bahwa bahasa mesin memiliki nilai biner atau dua nilai, kombinasi yang mewakili data. Kedua status ini adalah “Aktif (Active)” yang diwakili oleh 1 dan “Tidak Aktif (Inactive)” , diwakili oleh “0” . Karena itu setiap angka (nilai) diwakili dengan 0 dan 1 di sistem angka ini. Atau juga bisa diartikan sebagai 1 diartikan sebagai "Nyala" sedangkan 0 dinyatakan sebagai "Mati" dalam Sistem Bilangan Biner.
Sistem bilangan biner adalah sebuah sistem penulisan angka digital dimana hanya menggunakan dua simbol yaitu 0 dan 1. Sistem bilangan ini merupakan salah Satu dari Empat (1 dari 4) sistem bilangan yang digunakan komputer dimana 1 byte bilangan biner bernilai 8 bit. Bilangan biner juga diartikan sebagai sebuah bilangan yang menggunakan dua (2) Radiks atau basis yaitu 0 dan 1.
Pada Sistem Komputer Kode Biner dapat diartikan sebagai ukuran Komputasi sebuah data :
- 1 Byte = 8 bits (8 Digit Biner)
- 1 Kilobyte (KB) = 1000 Bytes (8000 bits)
- 1 Megabyte (MB) = 1.000.000 Bytes (1000 KB) (8.000.000 bits)
- 1 Gigabyte (GB) = 1.000.000.000 Bytes (1000 MB) (8 milyar bits)
- 1 Terabyte (TB) = 1 Triliun Bytes (1000 GB) (8 Triliun bits)
Contoh Bilangan Biner :
- 1111 0101
- 0011 1010
- 1101 0011
- 1010 1010
Mengapa Biner, mengapa bukan Desimal?
Menerapkan Secara Elektronik yaitu :
- 10 nilai yang berbeda sulit untuk disimpan. ENIAC (Elektronik pertama komputer) menggunakan 10 tabung vakum / digit
- Mereka sulit untuk ditransmisikan. Perlu presisi tinggi untuk mengkodekan 10 tingkat sinyal pada kabel tunggal.
- Berantakan untuk mengimplementasikan fungsi logika digital seperti penambahan, perkalian, dll.
1. Konvensi Bilangan Biner
Untuk mengkonversi setiap sistem bilangan entah itu Biner, Oktal, Desimal ataupun Heksadesimal sebenarnya sangat amat mudah asalkan kita tahu konsepnya.
- Bilangan Biner murupakan bilangan yang punya Dua Basis (0 dan 1)
- Bilangan Oktal murupakan bilangan yang punya Delapan Basis (0 s/d 7)
- Bilangan Desimal murupakan bilangan yang punya Sepuluh Basis (0 s/d 9)
- Bilangan Heksadesimal murupakan bilangan yang punya Enam Belas Basis (0 s/d F)
 |
| Tabel Konvensi Bilangan Biner, Oktal, Desimal, dan Heksadesimal |
Pengelompokan Biner dalam komputer selalu berjumlah 8, dengan istilah 1 Byte/Bita. Dalam istilah komputer, 1 Byte = 8 bit. Kode-kode rancang bangun komputer, seperti ASCII, American Standard Code for Information Interchange menggunakan sistem peng-kode-an 1 Byte.
20 = 1
21 = 2
22 = 4
23 = 8
24 = 16
25 = 32
26 = 64
dst.
Dalam sistem komunikasi digital modern, dimana data ditransmisikan dalam bentuk bit-bit biner, dibutuhkan Sistem yang tahan terhadap noise yang terdapat di kanal transmisi sehingga data yang ditransmisikan tersebut dapat diterima dengan benar. Kesalahan dalam pengiriman atau penerimaan data merupakan permasalahan yang mendasar yang memberikan dampak yang sangat signifikan pada sistem komunikasi. Biner yang biasa dipakai itu ada 8 Digit angka dan cuma berisikan angka 1 dan 0, tidak ada angka lainnya.
a. Biner ke Heksadesimal
Untuk memahami Konversi Bilangan Biner ke Bilangan Heksadesimal, silakan lihat Gambar (Infografik) di bawah ini :
Dan berikut, inilah beberapa Konversi dari Bilangan Biner ke Bilangan Heksadesimal :
Konversi untuk Bilangan Bulat :
b. Biner ke Desimal
Untuk memahami Konversi Bilangan Biner ke Bilangan Desimal, silakan lihat Gambar (Infografik) di bawah ini :
Dan berikut, inilah beberapa Konversi dari Bilangan Biner ke Bilangan Desimal :
Konversi untuk Bilangan Bulat :
Konversi untuk Bilangan Pecahan :
Konversi untuk Bilangan Campuran :
c. Biner ke Oktal
Proses ini kebalikan dari Algoritma sebelumnya. Digit biner dikelompokkan tiga, mulai dari bit paling signifikan dan melanjutkan ke kiri dan ke kanan. Tambahkan nol di depan (atau di belakang nol di sebelah kanan titik desimal) untuk mengisi kelompok tiga terakhir jika perlu. Kemudian ganti setiap trio dengan digit oktal yang setara.
Dan berikut, inilah beberapa Konversi dari Bilangan Biner ke Bilangan Oktal :
d. Biner ke Kuaterner
Untuk memahami Konversi Bilangan Biner ke Bilangan Kuaterner, silakan lihat Gambar (Infografik) di bawah ini :
Dan berikut, inilah beberapa Konversi dari Bilangan Biner ke Bilangan Kuaterner :
Pecahan dalam Aritmatika biner berakhir hanya jika 2 adalah satu-satunya faktor prima dalam penyebut. Akibatnya, 1/10 tidak memiliki representasi biner berhingga (10 memiliki faktor prima 2 dan 5). Hal ini menyebabkan 10 × 0,1 tidak sama persis dengan 1 dalam aritmatika titik-mengambang. Sebagai contoh, untuk menginterpretasikan ekspresi biner untuk 1/3 = .010101..., ini berarti: 1/3 = 0 × 2−1 + 1 × 2−2 + 0 × 2−3 + 1 × 2−4 + ... = 0,3125 + ... Nilai eksak tidak dapat ditemukan dengan jumlah berhingga pangkat dua, nol dan satu dalam representasi biner 1/3 bergantian selamanya.
Pecahan | Desimal | Biner | Pendekatan Pecahan |
| 1/1 | 1 or 0.999... | 1 or 0.111... | 1/2 + 1/4 + 1/8 ... |
| 1/2 | 0.5 or 0.4999... | 0.1 or 0.0111... | 1/4 + 1/8 + 1/16 ... |
| 1/3 | 0.333... | 0.010101... | 1/4 + 1/16 + 1/64 ... |
| 1/4 | 0.25 or 0.24999... | 0.01 or 0.00111... | 1/8 + 1/16 + 1/32 ... |
| 1/5 | 0.2 or 0.1999... | 0.00110011... | 1/8 + 1/16 + 1/128 ... |
| 1/6 | 0.1666... | 0.0010101... | 1/8 + 1/32 + 1/128 ... |
| 1/7 | 0.142857142857... | 0.001001... | 1/8 + 1/64 + 1/512 |
| 1/8 | 0.125 or 0.124999... | 0.001 or 0.000111... | 1/16 + 1/32 + 1/64 |
| 1/9 | 0.111... | 0.000111000111... | 1/16 + 1/32 + 1/64 . . |
| 1/10 | 0.1 or 0.0999... | 0.000110011... | 1/16 + 1/32 + 1/256 |
| 1/11 | 0.090909... | 0.00010111010001011101... | 1/16 + 1/64 + 1/128 |
| 1/12 | 0.08333... | 0.00010101... | 1/16 + 1/64 + 1/256 ... |
| 1/13 | 0.076923076923... | 0.000100111011000100111011... | 1/16 + 1/128 + 1/256 ... |
| 1/14 | 0.0714285714285... | 0.0001001001... | 1/16 + 1/128 + 1/1024 ... |
| 1/15 | 0.0666... | 0.00010001... | 1/16 + 1/256 ... |
| 1/16 | 0.0625 or 0.0624999... | 0.0001 or 0.0000111... | 1/32 + 1/64 + 1/128 ... |
3. Perhitungan (Kalkulasi) Bilangan Biner
Aritmatika dalam biner sangat mirip dengan Aritmatika dalam sistem angka lainnya. Penjumlahan, Pengurangan, Perkalian, dan Pembagian dapat dilakukan pada Bilangan Biner. Untuk, Penjumlahan dan Pengurangan Bilangan Biner sangat mirip dengan Aljabar Boolean dan Gerbang Logika.
Untuk lebih jelasnya, silakan lihat Infografik di bawah ini :
Penjumlahan :
Pengurangan :
Perkalian :
Pembagian :
Akar Kuadrat :
2. Bilangan Terner (Basis 3)
Sumber Artikel : Wikipedia.org
Terner (Juga disebut Basis 3 atau Ternary/Trinary) memiliki tiga sebagai basisnya. Analog dengan bit, digit Terner adalah trit (digit trinary). Satu trit setara dengan log2(3) (sekitar 1,58496) bit informasi.
Meskipun terner paling sering mengacu pada sistem di mana tiga digit semuanya adalah bilangan non-negatif; khususnya 0, 1, dan 2, kata sifat juga meminjamkan namanya ke sistem terner seimbang; terdiri dari digit 1, 0 dan +1, digunakan dalam logika perbandingan dan komputer ternary.
1. Konversi Bilangan
a. Terner ke Biner
Untuk memahami Konversi Bilangan Terner ke Bilangan Desimal, silakan lihat Gambar (Infografik) di bawah ini :
Dan berikut, inilah beberapa Konversi dari Bilangan Terner ke Bilangan Desimal :
Konversi untuk Bilangan Bulat :
2. Pecahan Terner
Adapun Bilangan Rasional, Terner menawarkan cara yang nyaman untuk mewakili
1/3 sama seperti Sener (berlawanan dengan rumitnya beberapa representasi sebagai string tak terbatas dari angka berulang dalam desimal); tetapi kelemahan utama adalah bahwa, pada gilirannya, Terner tidak menawarkan representasi terbatas untuk 1/2 (atau untuk 1/4, 1/8, dll.), karena 2 bukan faktor prima dari basis; seperti halnya basis dua, sepersepuluh (desimal 1/10, Sener 1/14) tidak dapat direpresentasikan secara tepat (yang akan membutuhkan misalnya desimal); juga bukan Seperenam (Sener 1/10, desimal 1/6).
3. Tabel Perkalian Terner
Representasi bilangan bulat dalam Ternary tidak terlalu panjang seperti dalam biner. Misalnya, desimal 365 atau senary 1405 sesuai dengan biner 101101101 (Sembilan digit) dan terner 111112 (enam digit). Namun, mereka masih jauh kurang kompak daripada representasi yang sesuai dalam basis seperti desimal - lihat di bawah untuk cara kompak untuk mengkodifikasi terner menggunakan Noner (Basis 9) dan Septemvigesimal (Basis 27).
Berikut inilah Tabel Perkalian untuk Sistem Bilangan Terner :
A Ternary Multiplication Table | |||||||||
| × | 1 | 2 | 10 | 11 | 12 | 20 | 21 | 22 | 100 |
| 1 | 1 | 2 | 10 | 11 | 12 | 20 | 21 | 22 | 100 |
| 2 | 2 | 11 | 20 | 22 | 101 | 110 | 112 | 121 | 200 |
| 10 | 10 | 20 | 100 | 110 | 120 | 200 | 210 | 220 | 1000 |
| 11 | 11 | 22 | 110 | 121 | 202 | 220 | 1001 | 1012 | 1100 |
| 12 | 12 | 101 | 120 | 202 | 221 | 1010 | 1022 | 1111 | 1200 |
| 20 | 20 | 110 | 200 | 220 | 1010 | 1100 | 1120 | 1210 | 2000 |
| 21 | 21 | 112 | 210 | 1001 | 1022 | 1120 | 1211 | 2002 | 2100 |
| 22 | 22 | 121 | 220 | 1012 | 1111 | 1210 | 2002 | 2101 | 2200 |
| 100 | 100 | 200 | 1000 | 1100 | 1200 | 2000 | 2100 | 2200 | 10000 |
4. Perhitungan (Kalkulasi) Bilangan Terner
Hampir sama seperti Bilangan Biner, Bilangan Terner juga hampir mendekati. Hanya saja perbedaannya adalah adanya Angka 2.
Untuk lebih jelasnya, silakan lihat Infografik di bawah ini :
3. Bilangan Kuaterner (Basis 4)
Sumber Artikel : Wikipedia.org
Sistem Bilangan Kuarterner adalah basis-4. Ini menggunakan angka 0, 1, 2 dan 3 untuk mewakili bilangan real apa pun. Konversi dari biner sangat mudah.
Empat adalah bilangan terbesar dalam rentang subitisasi dan salah satu dari dua bilangan yang merupakan bilangan kuadrat dan bilangan komposit tinggi (yang lainnya adalah 36), menjadikan kuaterner sebagai pilihan yang tepat untuk basis pada skala ini. Meskipun dua kali lebih besar, ekonomi radixnya sama dengan biner. Namun, tarifnya tidak lebih baik dalam pelokalan bilangan prima (basis terkecil yang lebih baik adalah basis primorial enam, senary).
Kuarter berbagi dengan semua sistem bilangan radix tetap banyak properti, seperti kemampuan untuk mewakili bilangan real apa pun dengan representasi kanonik (hampir unik) dan karakteristik representasi bilangan rasional dan bilangan irasional. Lihat desimal dan biner untuk diskusi tentang properti ini.
Angka 0 sampai 64 dalam Bilangan Kuartener Standar :
1. Konvensi Bilangan Kuaterner
Seperti halnya sistem bilangan oktal dan heksadesimal, kuartener memiliki hubungan khusus dengan sistem Bilangan Biner. Setiap Radix 4, 8 dan 16 adalah pangkat 2, jadi konversi ke dan dari biner dilakukan dengan mencocokkan setiap digit dengan 2, 3 atau 4 digit biner, atau bit.
a. Kuaterner ke Desimal
Untuk memahami Konversi Bilangan Kuaterner ke Bilangan Desimal, silakan lihat Gambar (Infografik) di bawah ini :
Dan berikut, inilah beberapa Konversi dari Bilangan Kuaterner ke Bilangan Desimal :
Konversi untuk Bilangan Bulat :
Konversi untuk Bilangan Pecahan :
Konversi untuk Bilangan Campuran :
b. Kuaterner ke Heksadesimal
Untuk memahami Konversi Bilangan Kuaterner ke Bilangan Heksadesimal, silakan lihat Gambar (Infografik) di bawah ini :
Dan berikut, inilah beberapa Konversi dari Bilangan Kuaterner ke Bilangan Heksadesimal :
Konversi untuk Bilangan Bulat :
Konversi untuk Bilangan Pecahan :
Konversi untuk Bilangan Campuran :
c. Kuaterner ke Oktal
Untuk memahami Konversi Bilangan Kuaterner ke Bilangan Oktal, silakan lihat Gambar (Infografik) di bawah ini :
Dan berikut, inilah beberapa Konversi dari Bilangan Kuaterner ke Bilangan Oktal :
Konversi untuk Bilangan Bulat :
Konversi untuk Bilangan Pecahan :
Konversi untuk Bilangan Campuran :
d. Kuaterner ke Biner
Untuk memahami Konversi Bilangan Kuaterner ke Bilangan Biner, silakan lihat Gambar (Infografik) di bawah ini :
Dan berikut, inilah beberapa Konversi dari Bilangan Kuaterner ke Bilangan Biner :
Konversi untuk Bilangan Bulat :
2. Pecahan Kuartener
Karena hanya memiliki Faktor Dua, banyak Pecahan Kuatener memiliki angka berulang, meskipun ini cenderung cukup sederhana :
3. Perhitungan (Kalkulasi) Bilangan Kuaterner
Merupakan Perhitungan Kalkulasi menggunakan Bilangan Kuaterner atau berbasis 4. Untuk lebih jelasnya, silakan lihat Infografik di bawah ini :
4. Bilangan Oktal (Basis 8)
Sumber Artikel : Wikipedia.org
Oktal atau sistem bilangan basis delapan adalah sebuah Sistem Bilangan berbasis 8 (Delapan). Simbol yang digunakan pada sistem ini adalah 0, 1, 2, 3, 4, 5, 6, 7. Konversi Sistem Bilangan Oktal berasal dari Sistem bilangan biner yang dikelompokkan tiap 3 (Tiga) bit biner dari ujung paling kanan (LSB atau Least Significant Bit).
Dalam Sistem Desimal, setiap tempat adalah Pangkat Sepuluh. Sebagai contoh :
Dalam Sistem Oktal, setiap tempat adalah Pangkat Delapan. Sebagai contoh :
Dengan melakukan perhitungan di atas dalam sistem desimal yang sudah dikenal, kita melihat mengapa 112 dalam oktal sama dengan 64+8+2 = 74 dalam desimal.
Angka Oktal dapat dengan mudah dikonversi dari representasi biner (mirip dengan sistem angka kuartener) dengan mengelompokkan digit biner berurutan ke dalam kelompok tiga (mulai dari kanan, untuk bilangan bulat). Misalnya, representasi biner untuk desimal 74 adalah 1001010. Dua angka nol dapat ditambahkan di sebelah kiri (00)1 001 010, yang sesuai dengan digit Oktal 1 1 2, menghasilkan representasi Oktal 112.
1. Konversi
a. Oktal ke Desimal
Untuk memahami Konversi Bilangan Oktal ke Bilangan Desimal, silakan lihat Gambar (Infografik) di bawah ini :
Dan berikut, inilah beberapa Konversi dari Bilangan Oktal ke Bilangan Desimal :
Untuk memahami Konversi Bilangan Oktal ke Bilangan Heksadesimal, silakan lihat Gambar (Infografik) di bawah ini :
Dan berikut, inilah beberapa Konversi dari Bilangan Oktal ke Bilangan Heksadesimal :
Konversi untuk Bilangan Bulat :
c. Oktal ke Kuaterner
Untuk memahami Konversi Bilangan Oktal ke Bilangan Kuaterner, silakan lihat Gambar (Infografik) di bawah ini :
d. Oktal ke Biner
Untuk memahami Konversi Bilangan Oktal ke Bilangan Biner, silakan lihat Gambar (Infografik) di bawah ini :
2. Pecahan Oktal
Karena hanya memiliki faktor dua, banyak Pecahan Oktal memiliki angka berulang, meskipun ini cenderung cukup sederhana :
a. Pecahan
Tabel di bawah ini memberikan ekspansi dari beberapa Bilangan Irasional umum dalam Desimal dan Oktal.
Bilangan | Representasi Posisi | |
Desimal | Oktal | |
| √2 (Panjang diagonal persegi satuan) | 1.414213562373095048... | 1.3240 4746 3177 1674... |
| √3 (Panjang diagonal kubus satuan) | 1.732050807568877293... | 1.5666 3656 4130 2312... |
| √5 (Panjang diagonal persegi panjang 1×2) | 2.236067977499789696... | 2.1706 7363 3457 7224... |
| φ ( | 1.618033988749894848... | 1.4743 3571 5627 7512... |
| π (pi, perbandingan keliling dengan diameter lingkaran) | 3.141592653589793238462643 383279502884197169399375105... | 3.1103 7552 4210 2643... |
| e (Basis untuk logaritma natural) | 2.718281828459045235... | 2.5576 0521 3050 5355... |
3. Perhitungan (Kalkulasi) Bilangan Oktal
Merupakan Perhitungan Kalkulasi menggunakan Bilangan Oktal atau berbasis 8. Untuk lebih jelasnya, silakan lihat Infografik di bawah ini :
Sumber Artikel : Wikipedia.org
Sistem bilangan desimal/persepuluhan adalah sistem bilangan yang menggunakan 10 macam angka dari 0,1, sampai 9. Setelah angka 9, angka berikutnya adalah 1 1, 1 2, dan seterusnya (posisi di angka 9 diganti dengan angka 0, 1, 3, .. 6 lagi, tetapi angka di depannya dinaikkan menjadi 1). sistem bilangan desimal ditemukan oleh Al-Kashi, Ilmuwan Persia.
Angka desimal (juga sering hanya desimal atau, kurang tepat, angka desimal), umumnya mengacu pada notasi angka dalam sistem angka desimal. Desimal kadang-kadang dapat diidentifikasi dengan pemisah desimal (biasanya "." atau "," seperti pada 25,9703 atau 3,1415). Desimal juga dapat merujuk secara khusus ke angka setelah pemisah desimal, seperti dalam "3.14 adalah perkiraan untuk dua desimal". Angka nol setelah pemisah desimal berfungsi untuk menandakan ketepatan suatu nilai.
Bilangan yang dapat direpresentasikan dalam sistem desimal adalah pecahan desimal. Yaitu, pecahan berbentuk a/10n, di mana a adalah bilangan bulat, dan n adalah bilangan bulat non-negatif.
Sistem desimal telah diperluas ke desimal tak terbatas untuk mewakili bilangan real apa pun, dengan menggunakan urutan angka tak terbatas setelah pemisah desimal (lihat representasi desimal). Dalam konteks ini, angka desimal dengan jumlah digit bukan nol yang terbatas setelah pemisah desimal kadang-kadang disebut desimal terminasi. Desimal berulang adalah desimal tak terbatas yang, setelah beberapa tempat, mengulangi urutan digit yang sama tanpa batas (mis., 5.123144144144144... = 5.123144). Desimal tak terbatas mewakili bilangan rasional, hasil bagi Dua bilangan bulat, jika dan hanya jika itu adalah desimal berulang atau memiliki jumlah digit bukan nol yang terbatas.
1. Konversi
a. Desimal ke Biner
Untuk memahami Konversi Bilangan Desimal ke Bilangan Biner, silakan lihat Gambar (Infografik) di bawah ini :
Dan berikut, inilah beberapa Konversi dari Bilangan Desimal ke Bilangan Biner :
Konversi untuk Bilangan Bulat :
Konversi untuk Bilangan Pecahan :
b. Desimal ke Terner
Untuk memahami Konversi Bilangan Desimal ke Bilangan Terner, silakan lihat Gambar (Infografik) di bawah ini :
c. Desimal ke Kuaterner
Untuk memahami Konversi Bilangan Desimal ke Bilangan Kuaterner, silakan lihat Gambar (Infografik) di bawah ini :
Dan berikut, inilah beberapa Konversi dari Bilangan Desimal ke Bilangan Kuaterner :
Konversi untuk Bilangan Bulat :
Konversi untuk Bilangan Pecahan :
Konversi untuk Bilangan Campuran :
d. Desimal ke Oktal
Untuk memahami Konversi Bilangan Desimal ke Bilangan Oktal, silakan lihat Gambar (Infografik) di bawah ini :
Dan berikut, inilah beberapa Konversi dari Bilangan Desimal ke Bilangan Oktal :
Konversi untuk Bilangan Bulat :
Untuk memahami Konversi Bilangan Desimal ke Bilangan Duodesimal, silakan lihat Gambar (Infografik) di bawah ini :
Dan berikut, inilah beberapa Konversi dari Bilangan Desimal ke Bilangan Duodesimal :
Konversi untuk Bilangan Bulat :
Konversi untuk Bilangan Pecahan :
Konversi untuk Bilangan Campuran :
f. Desimal ke Heksadesimal
Untuk memahami Konversi Bilangan Desimal ke Bilangan Heksadesimal, silakan lihat Gambar (Infografik) di bawah ini :
g. Desimal ke Vigesimal
Untuk memahami Konversi Bilangan Desimal ke Bilangan Vigesimal, silakan lihat Gambar (Infografik) di bawah ini :
h. Desimal ke Seksagesimal
Untuk memahami Konversi Bilangan Desimal ke Bilangan Seksagesimal, silakan lihat Gambar (Infografik) di bawah ini :
2. Notasi Desimal
Untuk menulis angka, sistem desimal menggunakan sepuluh angka desimal, tanda desimal, dan, untuk angka negatif, tanda minus "−". Angka desimal adalah 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; pemisah desimal adalah titik "." di banyak negara (kebanyakan berbahasa Inggris), dan koma "," di negara lain.
Untuk mewakili angka non-negatif, angka desimal terdiri dari :
a. salah satu urutan digit (terbatas) (seperti "2017"), di mana seluruh urutan mewakili bilangan bulat,
b. atau tanda desimal yang memisahkan dua urutan digit (seperti "20.70828")
Jika m > 0, yaitu, jika barisan pertama mengandung paling sedikit dua digit, maka umumnya diasumsikan bahwa digit pertama am bukan nol. Dalam beberapa keadaan mungkin berguna untuk memiliki satu atau lebih 0 di sebelah kiri; ini tidak mengubah nilai yang diwakili oleh desimal: misalnya, 3,14 = 03,14 = 003,14. Demikian pula, jika digit terakhir di sebelah kanan tanda desimal adalah nol—yaitu, jika bn = 0—mungkin dihapus; sebaliknya, angka nol yang tertinggal dapat ditambahkan setelah tanda desimal tanpa mengubah angka yang diwakili; misalnya, 15 = 15,0 = 15,00 dan 5,2 = 5,20 = 5,200.
Untuk mewakili angka negatif, tanda minus ditempatkan sebelum am. Angka mewakili angka :
Bagian bilangan bulat atau bagian integral dari angka desimal adalah bilangan bulat yang ditulis di sebelah kiri pemisah desimal (lihat juga pemotongan). Untuk bilangan desimal non-negatif, itu adalah bilangan bulat terbesar yang tidak lebih besar dari desimal. Bagian dari pemisah desimal ke kanan adalah bagian pecahan, yang sama dengan selisih antara bilangan dan bagian bilangan bulatnya.
Ketika bagian integral dari angka adalah nol, mungkin terjadi, biasanya dalam komputasi, bahwa bagian integer tidak ditulis (misalnya .1234, bukan 0.1234). Dalam penulisan normal, ini umumnya dihindari, karena risiko kebingungan antara tanda desimal dan tanda baca lainnya.
Singkatnya, kontribusi setiap digit terhadap nilai suatu bilangan tergantung pada posisinya dalam bilangan tersebut. Artinya, sistem desimal adalah sistem angka posisional.
3. Pecahan Desimal
Pecahan desimal (kadang-kadang disebut bilangan desimal, terutama dalam konteks yang melibatkan pecahan eksplisit) adalah bilangan rasional yang dapat dinyatakan sebagai pecahan yang penyebutnya adalah pangkat sepuluh. Misalnya, desimal mewakili pecahan 8/10, 1489/100, 24/100000, 1618/1000 dan 314159/100000, dan karenanya merupakan bilangan desimal.
Lebih umum, desimal dengan n digit setelah pemisah mewakili pecahan dengan penyebut 10n, yang pembilangnya adalah bilangan bulat yang diperoleh dengan menghapus pemisah.
Oleh karena itu, suatu bilangan adalah pecahan desimal jika dan hanya jika bilangan tersebut memiliki representasi desimal berhingga.
Dinyatakan sebagai pecahan tereduksi penuh, bilangan desimal adalah bilangan yang penyebutnya merupakan hasil kali pangkat 2 dan pangkat 5. Jadi, penyebut terkecil bilangan desimal adalah :
4. Bilangan Rasional
Pembagian panjang memungkinkan komputasi perluasan desimal tak terbatas dari bilangan rasional. Jika bilangan rasional adalah pecahan desimal, pembagian akhirnya berhenti, menghasilkan angka desimal, yang dapat diperpanjang menjadi perluasan tak terhingga dengan menambahkan angka nol tak terhingga banyaknya. Jika bilangan rasional bukan pecahan desimal, pembagian dapat dilanjutkan tanpa batas. Akan tetapi, karena semua sisa yang berurutan lebih kecil dari pembagi, hanya ada sejumlah sisa yang mungkin, dan setelah suatu tempat, urutan digit yang sama harus diulang tanpa batas waktu dalam hasil bagi. Artinya, seseorang memiliki desimal berulang. Misalnya,
1/81 = 0,012345679 012... (dengan grup 012345679 berulang tanpa batas).
Kebalikannya juga benar: jika, pada titik tertentu dalam representasi desimal suatu angka, rangkaian angka yang sama mulai berulang tanpa batas, angka tersebut rasional.
5. Perkiraan Bilangan Riil
Angka desimal tidak memungkinkan representasi yang tepat untuk semua bilangan real, mis. untuk bilangan real π. Namun demikian, mereka memungkinkan perkiraan setiap bilangan real dengan akurasi yang diinginkan, misalnya, desimal 3,14159 mendekati π nyata, kurang dari 10−5; jadi desimal banyak digunakan dalam sains, teknik, dan kehidupan sehari-hari.
Lebih tepatnya, untuk setiap bilangan real x dan setiap bilangan bulat positif n, terdapat dua desimal L dan u dengan paling banyak n digit setelah tanda desimal sehingga L ≤ x ≤ u dan (u − L) = 10−n.
Angka sangat sering diperoleh sebagai hasil pengukuran. Karena pengukuran tunduk pada ketidakpastian pengukuran dengan batas atas yang diketahui, hasil pengukuran direpresentasikan dengan baik oleh desimal dengan n digit setelah tanda desimal, segera setelah kesalahan pengukuran absolut dibatasi dari atas oleh 10−n. Dalam praktiknya, hasil pengukuran sering diberikan dengan angka tertentu setelah titik desimal, yang menunjukkan batas kesalahan. Misalnya, meskipun 0,080 dan 0,08 menunjukkan angka yang sama, angka desimal 0,080 menunjukkan pengukuran dengan kesalahan kurang dari 0,001, sedangkan angka 0,08 menunjukkan kesalahan absolut yang dibatasi oleh 0,01. Dalam kedua kasus, nilai sebenarnya dari besaran yang diukur bisa jadi, misalnya, 0,0803 atau 0,0796 (lihat juga angka signifikan).
6. Bilangan Duodesimal (Basis 12)
Sumber Artikel : Wikipedia.org
Sistem duodesimal (juga dikenal sebagai basis 12, Lusin, atau, jarang disebut sebagai Uncial) adalah sistem angka notasi posisi yang menggunakan dua belas sebagai basisnya. Angka dua belas (yaitu, angka yang ditulis sebagai "12" dalam sistem bilangan dasar sepuluh) malah ditulis sebagai "10" dalam duodesimal (artinya "1 lusin dan 0 satuan", bukannya "1 sepuluh dan 0 satuan") , sedangkan string digit "12" berarti "1 lusin dan 2 unit" (yaitu angka yang sama yang dalam desimal ditulis sebagai "14"). Demikian pula, dalam duodesimal "100" berarti "1 bruto", "1000" berarti "1 bruto besar", dan "0,1" berarti "1 per dua belas" (bukannya desimal berarti "seratus", "1 ribu", dan " 1 persepuluh").
Berbagai simbol telah digunakan untuk mewakili sepuluh dan sebelas dalam notasi duodesimal; halaman ini menggunakan A dan B, seperti dalam heksadesimal, yang membuat hitungan duodesimal dari nol hingga dua belas dibaca 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, 10.
Bilangan dua belas, bilangan komposit yang sangat unggul, adalah bilangan terkecil dengan Empat Faktor non-sepele (2, 3, 4, 6), dan yang terkecil untuk dimasukkan sebagai faktor keempat bilangan (1 hingga 4) dalam rentang Subitisasi, dan jumlah melimpah terkecil. Semua kelipatan kebalikan dari 3-bilangan halus (a⁄2b·3c di mana a, b, c adalah bilangan bulat) memiliki representasi terminasi dalam duodesimal. Secara khusus, +1⁄4 (0.3), +1⁄3 (0.4), +1⁄2 (0.6), +2⁄3 (0.8), dan +3⁄4 (0.9) semuanya memiliki representasi terminasi pendek dalam Perduabelas. Ada juga keteraturan yang lebih tinggi yang dapat diamati dalam tabel perkalian duodesimal. Akibatnya, duodesimal telah digambarkan sebagai sistem bilangan yang optimal.
Ini dianggap lebih unggul dari basis-10 (yang hanya memiliki 2 dan 5 sebagai faktor), dan juga untuk basis lain yang diusulkan seperti 16 atau 20. Basis-60 (dan basis-30 yang kurang populer) bahkan lebih baik dalam hal ini ( kebalikan dari semua angka 5-halus berakhir) tetapi dengan mengorbankan tabel perkalian yang sulit dan jumlah simbol yang jauh lebih besar untuk dihafal.
1. Sistem Bilangan
Simbol Transdesimal
Dalam sistem penomoran basis (Dua belas untuk duodesimal) harus ditulis sebagai 10, tetapi ada banyak usulan untuk bagaimana menulis duodesimal sepuluh dan sebelas.
Untuk memungkinkan entri pada mesin tik, huruf seperti A dan B (seperti dalam heksadesimal), T dan E (inisial Sepuluh dan Sebelas), X dan E (X dari angka Romawi untuk sepuluh), atau X dan Z digunakan. Beberapa menggunakan huruf Yunani seperti δ (singkatan untuk bahasa Yunani δέκα 'sepuluh') dan ε (untuk bahasa Yunani ένδεκα 'sebelas'), atau τ dan ε. Frank Emerson Andrews, seorang advokat Amerika awal untuk duodesimal, menyarankan dan menggunakan dalam bukunya New Numbers an X dan ℰ (script E, U+2130).
Edna Kramer dalam bukunya tahun 1951 The Main Stream of Mathematics menggunakan tanda bintang berujung enam (sextile) dan hash (atau octothorpe) #. Simbol dipilih karena tersedia pada beberapa mesin tik; mereka juga menggunakan telepon tombol-tekan. Notasi ini digunakan dalam publikasi Dozenal Society of America (DSA) dari 1974-2008.
Dari 2008 hingga 2015, DSA menggunakan ![]() dan
dan ![]() , simbol yang dirancang oleh William Addison Dwiggins.
, simbol yang dirancang oleh William Addison Dwiggins.
The Dozenal Society of Great Britain (DSGB) mengusulkan simbol yang diputar dua digit dan dibalik atau diputar tiga digit. Notasi ini, yang diturunkan dari angka Arab dengan rotasi 180 °, diperkenalkan oleh Isaac Pitman. Pada bulan Maret 2013, sebuah proposal diajukan untuk memasukkan formulir digit untuk sepuluh dan sebelas yang disebarkan oleh Dozenal Societies dalam Standar Unicode. Dari jumlah tersebut, bentuk British/Pitman diterima untuk pengkodean sebagai karakter pada titik kode U+218A ↊ TURNED DIGIT TWO dan U+218B ↋ TURNED DIGIT THREE. Mereka disertakan dalam rilis Unicode 8.0 pada Juni 2015 dan tersedia di LaTeX sebagai \textturntwo dan \textturnthree.
Setelah digit Pitman ditambahkan ke Unicode, DSA mengambil suara dan kemudian mulai menerbitkan konten menggunakan digit Pitman sebagai gantinya. Mereka masih menggunakan huruf X dan E dalam Teks ASCII. Karena karakter Unicode kurang didukung, halaman ini menggunakan "A" dan "B".
Proposal lain lebih kreatif atau estetis; misalnya, banyak yang tidak menggunakan angka Arab di bawah prinsip "identitas terpisah.
Notasi Basis
Ada juga berbagai proposal tentang cara membedakan bilangan duodesimal dari desimal. Mereka menyertakan huruf miring angka duodesimal "54 = 64", menambahkan "titik Humphrey" (titik koma, bukan titik desimal) ke angka duodesimal "54;6 = 64,5", atau kombinasi keduanya. Lainnya menggunakan subskrip atau label yang ditempelkan untuk menunjukkan basis, memungkinkan lebih dari desimal dan duodesimal untuk diwakili (untuk huruf tunggal 'z' dari "dozenal" digunakan sebagai 'd' berarti desimal) seperti "54z = 64d," "5412 = 6410" atau "doz 54 = dec 64."
2. Konversi
a. Duodesimal ke Terner
Dan berikut, inilah beberapa Konversi dari Bilangan Duodesimal ke Bilangan Terner :
Konversi untuk Bilangan Bulat :
Konversi untuk Bilangan Pecahan :
Konversi untuk Bilangan Campuran :
b. Duodesimal ke Desimal
Untuk memahami Konversi Bilangan Duodesimal ke Bilangan Desimal, silakan lihat Gambar (Infografik) di bawah ini :
Dan berikut, inilah beberapa Konversi dari Bilangan Duodesimal ke Bilangan Desimal :
Konversi untuk Bilangan Bulat :
Konversi untuk Bilangan Pecahan :
Konversi untuk Bilangan Campuran :
a. Duodesimal ke Heksadesimal
Dan berikut, inilah beberapa Konversi dari Bilangan Duodesimal ke Bilangan Heksadesimal :
Konversi untuk Bilangan Bulat :
Konversi untuk Bilangan Pecahan :
Konversi untuk Bilangan Campuran :
3. Pecahan Duodesimal
a. Pecahan
Pecahan Duodesimal mungkin sederhana :
Atau yang lebih rumit :
Seperti yang dijelaskan dalam desimal berulang, setiap kali pecahan yang tidak dapat direduksi ditulis dalam notasi titik radix dalam basis apa pun, pecahan dapat dinyatakan secara tepat (berakhir) jika dan hanya jika semua faktor prima dari penyebutnya juga merupakan faktor prima dari basis.
Karena 2 × 5 = 10, dalam sistem desimal, pecahan yang penyebutnya hanya terdiri dari kelipatan 2 dan 5 berakhir : 18 = 1(2×2×2), 120 = 1(2×2×5) dan 1500 = 1(2×2×5×5×5) dapat dinyatakan tepat sebagai 0,125, 0,05 dan 0,002 masing-masing. 13 dan 17, namun, berulang (0.333... dan 0.142857142857...).
Karena 2 × 2 × 3 = 12, dalam sistem duodesimal, 18 tepat; 120 dan 1500 berulang karena mereka memasukkan 5 sebagai faktor; 13 tepat; dan 17 berulang, seperti halnya dalam desimal.
b. Digit Berulang
The Dozenal Society of America berpendapat bahwa faktor 3 lebih sering ditemui dalam masalah pembagian kehidupan nyata daripada faktor 5. Jadi, dalam aplikasi praktis, gangguan desimal berulang lebih jarang ditemui ketika notasi duodesimal digunakan. Pendukung sistem duodesimal berpendapat bahwa ini terutama berlaku untuk perhitungan keuangan, di mana dua belas bulan dalam setahun sering dimasukkan ke dalam perhitungan.
Namun, ketika pecahan berulang terjadi dalam notasi duodesimal, mereka cenderung memiliki periode yang sangat pendek daripada dalam notasi desimal, karena 12 (Dua Belas) berada di antara dua bilangan prima, 11 (Sebelas) dan 13 (Tiga Belas), sedangkan sepuluh adalah berdekatan dengan bilangan komposit 9. Meskipun demikian, memiliki periode yang lebih pendek atau lebih lama tidak membantu ketidaknyamanan utama bahwa seseorang tidak mendapatkan representasi yang terbatas untuk pecahan tersebut dalam basis yang diberikan (jadi pembulatan, yang memperkenalkan ketidaktepatan, diperlukan untuk menanganinya dalam perhitungan), dan secara keseluruhan lebih mungkin untuk berurusan dengan angka berulang tak terbatas ketika pecahan dinyatakan dalam desimal daripada dalam duodesimal, karena satu dari setiap tiga bilangan berurutan mengandung faktor prima 3 dalam faktorisasinya, sedangkan hanya satu dari setiap lima mengandung faktor prima 5. Semua faktor prima lainnya, kecuali 2, tidak dibagi oleh sepuluh atau dua belas, sehingga mereka tidak mempengaruhi kemungkinan relatif untuk menemukan angka berulang (setiap pecahan yang dapat direduksi yang mengandung salah satu dari faktor-faktor lain ini dalam penyebutnya akan muncul kembali di salah satu basis).
Juga, faktor prima 2 muncul dua kali dalam faktorisasi dua belas, sedangkan hanya sekali dalam faktorisasi sepuluh; yang berarti bahwa sebagian besar pecahan yang penyebutnya merupakan pangkat dua akan memiliki representasi penghentian yang lebih pendek dan lebih mudah dalam duodesimal daripada dalam desimal :
- 1/(22) = 0.2510 = 0.312
- 1/(23) = 0.12510 = 0.1612
- 1/(24) = 0.062510 = 0.0912
- 1/(25) = 0.0312510 = 0.04612
Panjang Periode Duodesimal dari 1/n adalah (Dalam Basis 10) :
0, 0, 0, 0, 4, 0, 6, 0, 0, 4, 1, 0, 2, 6, 4, 0, 16, 0, 6, 4, 6, 1, 11, 0, 20, 2, 0, 6, 4, 4, 30, 0, 1, 16, 12, 0, 9, 6, 2, 4, 40, 6, 42, 1, 4, 11, 23, 0, 42, 20, 16, 2, 52, 0, 4, 6, 6, 4, 29, 4, 15, 30, 6, 0, 4, 1, 66, 16, 11, 12, 35, 0, ... (Urutan A246004 di OEIS)
Panjang Periode Duodesimal dari 1/(n prima) adalah (Dalam Basis 10) :
0, 0, 4, 6, 1, 2, 16, 6, 11, 4, 30, 9, 40, 42, 23, 52, 29, 15, 66, 35, 36, 26, 41, 8, 16, 100, 102, 53, 54, 112, 126, 65, 136, 138, 148, 150, 3, 162, 83, 172, 89, 90, 95, 24, 196, 66, 14, 222, 113, 114, 8, 119, 120, 125, 256, 131, 268, 54, 138, 280, ... (Urutan A246489 di OEIS)
Prima terkecil dengan periode duodesimal n adalah (Dalam Basis 10) :
11, 13, 157, 5, 22621, 7, 659, 89, 37, 19141, 23, 20593, 477517, 211, 61, 17, 2693651, 1657, 29043636306420266077, 85403261, 8177824843189, 57154490053, 47, 193, 303551, 79, 306829, 673, 59, 31, 373, 153953, 886381, 2551, 71, 73, ... (Urutan A252170 di OEIS)
c. Bilangan Irasional
Representasi bilangan irasional dalam sistem bilangan posisi apa pun (termasuk desimal dan duodesimal) tidak berakhir atau berulang. Tabel berikut memberikan digit pertama untuk beberapa bilangan aljabar dan transendental penting dalam desimal dan duodesimal.
| Algebraic irrational number | In decimal | In duodecimal |
|---|---|---|
| √2, the square root of 2 | 1.414213562373... | 1;4B79170A07B8... |
| φ (phi), the golden ratio = | 1.618033988749... | 1;74BB6772802A... |
| Transcendental number | In decimal | In duodecimal |
| π (pi), the ratio of a circle's circumference to its diameter | 3.141592653589... | 3;184809493B91... |
| e, the base of the natural logarithm | 2.718281828459... | 2;875236069821... |
4. Tabel Perkalian Duodesimal
5. Perhitungan (Kalkulasi) Bilangan Duodesimal
Merupakan Perhitungan Kalkulasi menggunakan Bilangan Duodesimal atau berbasis 12. Untuk lebih jelasnya, silakan lihat Infografik di bawah ini :
Sumber Artikel : Wikipedia.org dan Byjus.com
Dalam Matematika dan Komputasi, sistem Bilangan Heksadesimal (Juga basis 16 atau Hex) adalah sistem bilangan posisional yang mewakili angka menggunakan radix (basis) dari 16. Tidak seperti cara umum untuk mewakili angka menggunakan 10 simbol, Heksadesimal menggunakan 16 simbol yang berbeda, paling sering simbol "0"–"9" untuk mewakili nilai 0 hingga 9, dan "A"–"F" (atau alternatifnya "a"–"f") untuk mewakili nilai 10 hingga 15.
Angka heksadesimal banyak digunakan oleh perancang dan pemrogram sistem komputer karena memberikan representasi nilai kode biner yang ramah manusia. Setiap digit heksadesimal mewakili Empat bit (Digit Biner), juga dikenal sebagai nibble (atau nybble), yaitu 1/2 byte. Misalnya, satu byte dapat memiliki nilai mulai dari 00000000 hingga 11111111 dalam bentuk biner, yang dapat dengan mudah direpresentasikan sebagai 00 hingga FF dalam heksadesimal.
Dalam matematika, subscript biasanya digunakan untuk menentukan basis. Misalnya, nilai desimal 15.856 akan dinyatakan dalam Heksadesimal sebagai 3DF016. Dalam pemrograman, sejumlah notasi digunakan untuk menunjukkan bilangan heksadesimal, biasanya melibatkan awalan atau akhiran. Awalan 0x digunakan dalam C dan bahasa pemrograman terkait, yang akan menunjukkan nilai ini sebagai 0x3DF0.
Heksadesimal digunakan dalam pengkodean transfer Base16, di mana setiap byte plaintext dipecah menjadi dua nilai 4-bit dan diwakili oleh dua digit heksadesimal.
1. Konversi
a. Heksadesimal ke Desimal
Untuk memahami Konversi Bilangan Heksadesimal ke Bilangan Desimal, silakan lihat Gambar (Infografik) di bawah ini :
Dan berikut, inilah beberapa Konversi dari Bilangan Heksadesimal ke Bilangan Desimal :
b. Heksadesimal ke Duodesimal
Dan berikut, inilah beberapa Konversi dari Bilangan Heksadesimal ke Bilangan Duodesimal :
Konversi untuk Bilangan Bulat :
Konversi untuk Bilangan Pecahan :
Konversi untuk Bilangan Campuran :
c. Heksadesimal ke Oktal
Untuk memahami Konversi Bilangan Heksadesimal ke Bilangan Oktal, silakan lihat Gambar (Infografik) di bawah ini :
d. Heksadesimal ke Kuaterner
Untuk memahami Konversi Bilangan Heksadesimal ke Bilangan Kuaterner, silakan lihat Gambar (Infografik) di bawah ini :
e. Heksadesimal ke Biner
Untuk memahami Konversi Bilangan Heksadesimal ke Bilangan Biner, silakan lihat Gambar (Infografik) di bawah ini :
2. Pecahan Heksadesimal
a. Bilangan Rasional
Seperti sistem bilangan lainnya, sistem heksadesimal dapat digunakan untuk menyatakan bilangan rasional, meskipun pemuaian berulang sering terjadi karena enam belas (1016) hanya memiliki satu faktor prima; dua.
Untuk basis apa pun, 0,1 (atau "1/10") selalu setara dengan satu dibagi dengan representasi nilai basis itu dalam sistem bilangannya sendiri. Jadi, apakah membagi satu dengan dua untuk biner atau membagi satu dengan enam belas untuk heksadesimal, kedua pecahan ini ditulis sebagai 0,1 atau 0.1. Karena radix 16 adalah kuadrat sempurna (42), pecahan yang dinyatakan dalam heksadesimal memiliki periode ganjil lebih sering daripada desimal, dan tidak ada bilangan siklik (selain digit tunggal yang sepele). Digit berulang ditampilkan ketika penyebut dalam suku terendah memiliki faktor prima yang tidak ditemukan dalam radix; jadi, saat menggunakan notasi heksadesimal, semua pecahan dengan penyebut yang bukan merupakan pangkat dua menghasilkan rangkaian angka berulang yang tak terhingga (seperti pertiga dan perlima). Hal ini membuat heksadesimal (dan biner) kurang nyaman daripada desimal untuk mewakili bilangan rasional karena proporsi yang lebih besar berada di luar jangkauan representasi terbatasnya.
Semua bilangan rasional yang dapat diwakili hingga dalam heksadesimal juga dapat diwakili secara terbatas dalam desimal, duodesimal, dan sexagesimal: yaitu, setiap bilangan heksadesimal dengan jumlah digit yang terbatas juga memiliki jumlah digit yang terbatas ketika dinyatakan dalam basis lain tersebut. Sebaliknya, hanya sebagian kecil dari mereka yang dapat diwakili secara terbatas dalam basis terakhir yang dapat diwakili secara terbatas dalam heksadesimal. Misalnya, desimal 0,1 sesuai dengan representasi berulang tak terbatas 0.1 9 dalam heksadesimal. Namun, heksadesimal lebih efisien daripada duodesimal dan sexagesimal untuk mewakili pecahan dengan kekuatan dua dalam penyebut. Misalnya, 0.062510 (Seperenam belas) sama dengan 0.116, 0.0912, dan 0;3,4560 ().
b. Bilangan Irasional
Tabel di bawah ini memberikan perluasan beberapa Bilangan Irasional umum dalam Desimal dan Heksadesimal.
Number | Positional representation | |
Decimal | Hexadecimal | |
1.414213562373095048... | 1.6A09E667F3BCD... | |
1.732050807568877293... | 1.BB67AE8584CAA... | |
2.236067977499789696... | 2.3C6EF372FE95... | |
φ (phi, the golden ratio = (1+√5)/2) | 1.618033988749894848... | 1.9E3779B97F4A... |
π (pi, the ratio of circumference to diameter of a circle) | 3.141592653589793238462643 383279502884197169399375105... | 3.243F6A8885A308D313198A2E0 3707344A4093822299F31D008... |
e (the base of the natural logarithm) | 2.718281828459045235... | 2.B7E151628AED2A6B... |
τ (the Thue–Morse constant) | 0.412454033640107597... | 0.6996 9669 9669 6996... |
γ (the limiting difference between the harmonic series and the natural logarithm) | 0.577215664901532860... | 0.93C467E37DB0C7A4D1B... |
3. Tabel Perkalian Heksadesimal
Berikut inilah Tabel Perkalian untuk Sistem Bilangan Heksadesimal :
Dan inilah bentuk lain Tabel Perkalian dari Bilangan Heksadesimal (Dikembangkan oleh Elder Futhark) :
 |
| Elder Futhark Hexadecimal Multiplication Table |
4. Perhitungan (Kalkulasi) Bilangan Heksadesimal
Merupakan Perhitungan Kalkulasi menggunakan Bilangan Heksadesimal atau berbasis 16. Untuk lebih jelasnya, silakan lihat Infografik di bawah ini :
8. Bilangan Vigesimal (Basis 20)
Sumber Artikel : Wikipedia.org
1. Sistem Bilangan
Biasanya Sistem Bilangan Vigesimal dipakai pada Zaman Mesoamerika seperti Suku Maya dan Nahuatl (Suku Aztec/Aztek)
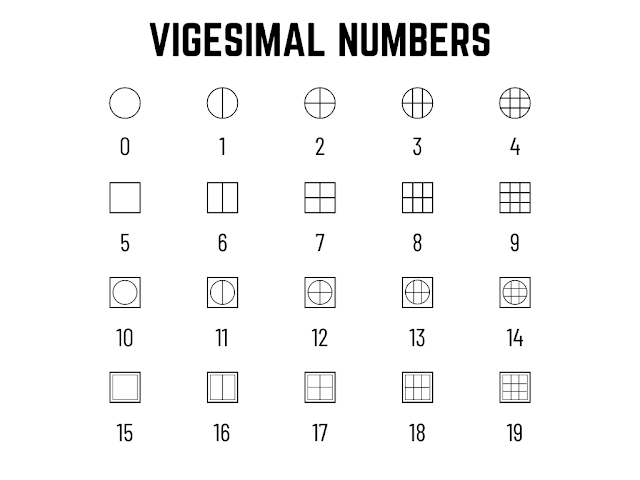 |
| Bilangan Vigesimal dengan Angka |
 |
| Bilangan Vigesimal dengan Angka dan Huruf (Karakter) |
Akan tetapi, Bilangan Vigesimal diatas merupakan Hasil Modifikasi saya sendiri.
2. Konversi Bilangan
a. Vigesimal ke Desimal
Untuk memahami Konversi Bilangan Vigesimal ke Bilangan Desimal, silakan lihat Gambar (Infografik) di bawah ini :
3. Pecahan Vigesimal
a. Bilangan Pecahan
Karena 20 habis dibagi dua dan lima dan berbatasan dengan 21, hasil kali tiga dan tujuh, sehingga mencakup empat bilangan prima pertama, banyak pecahan vigesimal memiliki representasi sederhana, baik penghentian atau pengulangan (walaupun pertiga lebih rumit daripada desimal, mengulangi dua digit, bukan satu). Dalam desimal, membagi tiga dua kali (sembilan) hanya memberikan satu digit periode (1/9 = 0,1111.... misalnya) karena 9 adalah angka di bawah sepuluh. 21, namun, bilangan yang berdekatan dengan 20 yang habis dibagi 3, tidak habis dibagi 9. Persembilan dalam Vigesimal memiliki periode enam digit. Karena 20 memiliki faktor prima yang sama dengan 10 (dua dan lima), pecahan akan berakhir dalam desimal jika dan hanya jika berakhir dalam Vigesimal.
Menggunakan Angka Khusus (Pecahan Tidak Berulang) :
Menggunakan Angka Khusus (Pecahan Berulang) :b. Bilangan Irasional
Faktorisasi prima dari dua puluh adalah 22 × 5, jadi ini bukan pangkat sempurna. Namun, bagian bebas perseginya, 5, kongruen dengan 1 (mod 4). Jadi, menurut dugaan Artin tentang akar primitif, vigesimal memiliki bilangan prima siklik yang jumlahnya tak terhingga, namun pecahan bilangan prima yang siklik belum tentu ~37,395%. Program UnrealScript yang menghitung lama periode berulang berbagai pecahan dalam himpunan basis tertentu menemukan bahwa, dari 15.456 bilangan prima pertama, ~39,344% merupakan siklik dalam vigesimal.
| Bilangan Aljabar Irasional | Dalam Desimal | Dalam Vigesimal |
|---|---|---|
| √2 (the length of the diagonal of a unit square) | 1.41421356237309... | 1.85DE37JGF09H6... |
| √3 (the length of the diagonal of a unit cube) | 1.73205080756887... | 1.ECG82BDDF5617... |
| √5 (the length of the diagonal of a 1 × 2 rectangle) | 2.2360679774997... | 2.4E8AHAB3JHGIB... |
| φ (phi, the Golden Ratio = 1+√52) | 1.6180339887498... | 1.C7458F5BJII95... |
| Transcendental irrational number | Dalam Desimal | Dalam Vigesimal |
| π (pi, the ratio of circumference to diameter) | 3.14159265358979... | 3.2GCEG9GBHJ9D2... |
| e (the base of the natural logarithm) | 2.7182818284590452... | 2.E7651H08B0C95... |
| γ (the pi between the harmonic series and the natural logarithm 2) | 0.5772156649015328606... | 0.BAHEA2B19BDIBI... |
4. Tabel Perkalian Vigesimal
Inilah Tabel Perkalian Vigesimal :
Merupakan Perhitungan Kalkulasi menggunakan Bilangan Vigesimal atau berbasis 20. Untuk lebih jelasnya, silakan lihat Infografik di bawah ini :
9. Bilangan Seksagesimal (Basis 60)
Sumber Artikel : Wikipedia.org
1. Sistem Bilangan (Kegunaan)
 |
| Angka Seksagesimal Babilonia |
Sistem sexagesimal seperti yang digunakan di Mesopotamia kuno bukanlah sistem basis-60 murni, dalam arti bahwa ia tidak menggunakan 60 simbol yang berbeda untuk angka-angkanya. Sebaliknya, angka paku menggunakan sepuluh sebagai sub-basis dalam mode notasi nilai tanda angka Seksagesimal terdiri dari sekelompok tanda berbentuk baji sempit yang mewakili unit hingga sembilan (![]() ,
, ![]() ,
, ![]() ,
, ![]() , ...,
, ..., ![]() ) dan sekelompok tanda lebar berbentuk baji yang mewakili hingga lima puluhan (
) dan sekelompok tanda lebar berbentuk baji yang mewakili hingga lima puluhan (![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ). Nilai digit adalah jumlah dari nilai bagian-bagian komponennya ada pada gambar di atas.
). Nilai digit adalah jumlah dari nilai bagian-bagian komponennya ada pada gambar di atas.
Angka yang lebih besar dari 59 ditunjukkan oleh beberapa blok simbol dari bentuk ini dalam notasi nilai tempat. Karena tidak ada simbol untuk nol, tidak selalu jelas bagaimana suatu bilangan harus ditafsirkan, dan nilai sebenarnya kadang-kadang harus ditentukan oleh konteksnya. Misalnya, simbol untuk 1 dan 60 adalah identik. Kemudian teks Babilonia menggunakan placeholder (![]() ) untuk mewakili nol, tetapi hanya di posisi tengah, dan bukan di sisi kanan nomor, seperti yang kita lakukan dalam Angka seperti 13200.
) untuk mewakili nol, tetapi hanya di posisi tengah, dan bukan di sisi kanan nomor, seperti yang kita lakukan dalam Angka seperti 13200.
Dan inilah Sistem Bilangan Seksagesimal yang saya modifikasi :
 |
| Bilangan Seksagesimal Turus (Modifikasi dari Angka Babilonia) |
Penggunaan modern untuk sistem Seksagesimal termasuk mengukur sudut, koordinat geografis, navigasi elektronik, dan waktu.
Satu jam waktu dibagi menjadi 60 Menit, dan satu menit dibagi menjadi 60 detik. Dengan demikian, pengukuran waktu seperti 3:23:17 (3 Jam, 23 Menit, dan 17 Detik) dapat diartikan sebagai bilangan Seksagesimal utuh (tanpa titik Seksagesimal), artinya 3 × 602 + 23 × 601 + 17 × 600 detik. Namun, masing-masing dari tiga digit Seksagesimal dalam angka ini (3, 23, dan 17) ditulis menggunakan sistem desimal.
Demikian pula, satuan praktis ukuran sudut adalah derajat, yang ada 360 (Tiga Enam Puluh) dalam Lingkaran. Ada 60 Menit busur dalam satu derajat, dan 60 Detik busur dalam satu menit.
2. Konversi
a. Seksagesimal ke Desimal
Untuk memahami Konversi Bilangan Seksagesimal ke Bilangan Desimal, silakan lihat Gambar (Infografik) di bawah ini :
3. Pecahan Seksagesimal
a. Bilangan Pecahan
Dalam Sistem Seksagesimal, setiap pecahan di mana penyebutnya adalah bilangan biasa (hanya memiliki 2, 3, dan 5 dalam Faktorisasi primanya) dapat dinyatakan dengan tepat. Berikut ini adalah semua pecahan jenis ini yang penyebutnya kurang dari atau sama dengan 60 :
Namun bilangan yang tidak beraturan membentuk pecahan berulang yang lebih rumit. Sebagai contoh :
Fakta bahwa dua bilangan yang berdekatan dengan 60, 59 dan 61, keduanya merupakan bilangan prima menyiratkan bahwa pecahan yang berulang dengan periode satu atau dua digit sexagesimal hanya dapat memiliki kelipatan bilangan beraturan 59 atau 61 sebagai penyebutnya, dan bahwa bilangan tidak beraturan lainnya memiliki pecahan yang berulang dengan periode yang lebih lama.
b. Bilangan Irasional
Representasi bilangan irasional dalam sistem bilangan posisional apa pun (termasuk desimal dan seksagesimal) tidak berakhir atau berulang.
Akar kuadrat dari 2, panjang diagonal suatu satuan persegi, diperkirakan oleh orang Babilonia pada Periode Babilonia Lama (1900 SM – 1650 SM) sebagai :
Nilai π yang digunakan oleh matematikawan dan ilmuwan Yunani Ptolemy adalah 3;8,30 = 3 + 8/60 + 30/602 = 377/120 ≈ 3.141666.... Jamshīd al-Kāshī, seorang matematikawan Persia abad ke-15 , dihitung 2π sebagai ekspresi seksagesimal ke nilai yang benar jika dibulatkan menjadi 9 (Sembilan) Subdigit (jadi menjadi 1/609); nilainya untuk 2π adalah :
6;16,59,28,1,34,51,46,14,50. Seperti √2 di atas, 2π merupakan bilangan irasional dan tidak dapat dinyatakan secara eksak dalam sexagesimal. Ekspansi seksagesimalnya dimulai 6;16,59,28,1,34,51,46,14,49,55,12,35... (OEIS: A091649)
4. Tabel Perkalian Seksagesimal
Berikut, inilah Tabel Perkalian untuk Bilangan Seksagesimal :
 |
| Tabel Perkalian Seksagesimal Versi Jam (Klik Gambar untuk melihat dan memperjelas Gambar) |
.png) |
| Tabel Perkalian Seksagesimal dengan menggunakan Karakter Angka dan Huruf (Klik Gambar untuk melihat dan memperjelas Gambar) |
Atau yang ini Tabel Perkalian untuk Bilangan Seksagesimal :
5. Perhitungan (Kalkulasi) Bilangan Seksagesimal
Merupakan Perhitungan Kalkulasi menggunakan Bilangan Seksagesimal atau berbasis 60. Untuk lebih jelasnya, silakan lihat Infografik di bawah ini :
[SEGERA / COMING SOON]
Untuk selengkapnya terkait dengan Bilangan Seksagesimal, silakan lihat di sini :
CARA MENGKONVERSIKAN SISTEM BILANGAN APAPUN
1. Dengan menggunakan Wolfram Alpha
Pertama, bukalah Situs Wolfram|Alpha. Kemudian, ketiklah Angka yang ingin kalian Input. Yang perlu kita ketahui adalah jika kita ingin mengonversikan Sistem Bilangan melalui Wolfram Alpha, maka kita hanya bisa melakukan Konversi dari Bilangan Desimal saja. Akan tetapi, dalam kondisi tertentu kita dapat melakukan Konversi dari Bilangan Biner, Oktal, ataupun Heksadesimal saja. Untuk Referensi, silakan lihat di sini.
1. Dari Bilangan Desimal
Berikut, inilah beberapa contoh Konversi Bilangan Desimal dari Bilangan Biner sampai berapapun.
1. 80 in Binary
7. 268343 in Vigesimal
9. 12864150 in Sexagesimal
2. Ke Bilangan Desimal
Yang perlu kita ketahui adalah kita hanya bisa melakukan Konversi Bilangan dari Biner sampai Heksatrigesimal (Basis 36).
1. (110110 base 2) to Decimal
2. (120212 base 3) to Decimal
3. (320213 base 4) to Decimal
4. (24130 base 5) to Decimal
8. (8DFC base 16) to Decimal
9. (G1IJ base 20) to Decimal
Dengan ChatGPT, kita bisa bertanya secara bebas untuk mengonversi Sistem Bilangan apapun. Akan tetapi yang perlu diingat bahwa, jika kita tanyakan secara langsung tentang Cara mengonversi Sistem Bilangan, maka ChatGPT akan langsung membuatkan dalam bentuk Pemrograman Python. Akan tetapi, kita tidak butuh kode programnya dan hanya membutuhkan konversinya saja.
Contoh Prompt Pertama :
Convert 240 to Hexadecimal! (Manual Count without Python Code!)
Hasil :
Contoh Prompt Kedua :
Convert these Numbers From Decimal to Vigesimal! - 45620 - 0.3891 - 6278.1974 Convert these Numbers From Vigesimal to Decimal! - HJI3 - 0.75AC - 8DF.3BEG
Hasil :
3. Dengan menggunakan Bahasa Pemrograman
Sumber : Geeksforgeeks.org
Biarkan Angka desimal input yang diberikan menjadi "inputNum" dan basis target menjadi "base". Kami berulang kali membagi inputNum dengan basis dan menyimpan sisanya. Kami akhirnya membalikkan string yang diperoleh. Di bawah ini adalah implementasi dalam beberapa Bahasa Pemrograman.
Contoh Input/Output :
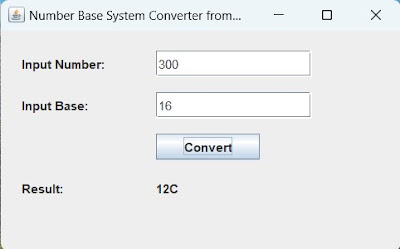
Konversi Sistem Bilangan dari Desimal Number Base System Converter from Decimal =========================================== Input Number : 256 Input Base : 16 256 [ 16 ] = 100
- Kompleksitas Waktu : O(N) Mengonversi angka input diberikan "base" dengan input "inputNum" membaginya dengan basis dan mengambil sisanya membutuhkan kompleksitas O(n).
- Ruang Bantu : O(1)
1. C
#include <stdio.h>#include <string.h>char reVal(int num){if (num >= 0 && num <= 9){return (char)(num + '0');}else {return (char)(num - 10 + 'A');}}void strev(char *str){int len = strlen(str);int i;for (i = 0; i < len/2; i++){char temp = str[i];str[i] = str[len-i-1];str[len-i-1] = temp;}}char* fromDeci(char res[], int base, int inputNum){int index = 0;while (inputNum > 0){res[index++] = reVal(inputNum % base);inputNum /= base;}res[index] = '\0';strev(res);return res;}int main(){printf("Konversi Sistem Bilangan dari Desimal\n");printf("Number Base System Converter from Decimal\n");printf("===========================================\n");char res[100];int inputNum, base;printf("Input Number : ");scanf("%d", &inputNum);printf("Input Base : ");scanf("%d", &base);printf("%d[%d] = %s\n", inputNum, base, fromDeci(res, base, inputNum));return 0;}
2. C++
#include <bits/stdc++.h>using namespace std;char reVal(int num){if (num >= 0 && num <= 9) {return (char)(num + '0');}else {return (char)(num - 10 + 'A');}}string fromDeci(string& res, int base, int inputNum){int index = 0;while (inputNum > 0) {res.push_back(reVal(inputNum % base));index++;inputNum /= base;}reverse(res.begin(), res.end());return res;}int main(){cout<<"Konversi Sistem Bilangan dari Desimal"<<endl;cout<<"Number Base System Converter from Decimal"<<endl;cout<<"==========================================="<<endl;string res;int inputNum, base;cout<<"Input Number : ";cin>>inputNum;cout<<"Input Base : ";cin>>base;cout<<inputNum<<"["<<base<<"] = "<<fromDeci(res, base, inputNum)<<endl;return 0;}
3. C#
using System;class NumberSystemConversion {static char reVal(int num){if (num >= 0 && num <= 9)return (char)(num + 48);elsereturn (char)(num - 10 + 65);}static string fromDeci(int bse, int inputNum){string s = "";while (inputNum > 0){s += reVal(inputNum % bse);inputNum /= bse;}char[] res = s.ToCharArray();Array.Reverse(res);return new String(res);}static void Main(){Console.WriteLine("Konversi Sistem Bilangan dari Desimal");Console.WriteLine("Number Base System Converter from Decimal");Console.WriteLine("===========================================");int inputNum, bse;Console.Write("Input Number : ");inputNum = Console.Read();Console.Write("Input Base : ");bse = Console.Read();Console.WriteLine(inputNum+"["+bse+"] = "+fromDeci(bse, inputNum));}}
4. Java
import java.lang.*;import java.io.*;import java.util.*;class NumberSystemConversion {static char reVal(int num){if (num >= 0 && num <= 9) {return (char)(num + 48);}else {return (char)(num - 10 + 65);}}static String fromDeci(int bse, int inputNum){String s = "";while (inputNum > 0){s += reVal(inputNum % bse);inputNum /= bse;}StringBuilder ix = new StringBuilder();ix.append(s);return new String(ix.reverse());}public static void main (String[] args){System.out.println("Konversi Sistem Bilangan dari Desimal");System.out.println("Number Base System Converter from Decimal");System.out.println("===========================================");Scanner scan = new Scanner(System.in);int inputNum, bse;System.out.print("Input Number : ");inputNum = scan.nextInt();System.out.print("Input Base : ");bse = scan.nextInt();System.out.println(inputNum+"["+bse+"] = "+fromDeci(bse, inputNum));}}
5. Python
def reVal(num):if (num >= 0 and num <= 9):return chr(num + ord('0'))else:return chr(num - 10 + ord('A'))def strev(str):len = len(str)for i in range(int(len / 2)):temp = str[i]str[i] = str[len - i - 1]str[len - i - 1] = tempdef fromDeci(res, base, inputNum):index = 0while (inputNum > 0):res+= reVal(inputNum % base)inputNum = int(inputNum / base)res = res[::-1]return resprint("Konversi Sistem Bilangan dari Desimal")print("Number Base System Converter from Decimal")print("===========================================")inputNum = int(input("Input Number : "))base = int(input("Input Base : "))res = ""print(inputNum,"[",base,"] = ",fromDeci(res, base, inputNum))
6. JavaScript (Node.JS)
function reVal(num) {if (num >= 0 && num <= 9) return String.fromCharCode(num + 48);else return String.fromCharCode(num - 10 + 65);}function fromDeci(base1, inputNum) {let s = "";while (inputNum > 0) {s += reVal(inputNum % base1);inputNum = parseInt(inputNum / base1, 10);}let res = s.split("");res.reverse();return res.join("");}console.log("Konversi Sistem Bilangan dari Desimal");console.log("Number Base System Converter from Decimal");console.log("===========================================");const prompt = require("prompt-sync")(); // some compiler are required this sectionlet inputNum = prompt("Input Number : ");let base1 = prompt("Input Base : ");console.log(inputNum + "[" + base1 + "] = " + fromDeci(base1, inputNum));
7. Dart
import 'dart:io';String reVal(int num) {if (num >= 0 && num <= 9) {return String.fromCharCode(num + '0'.codeUnitAt(0));} else {return String.fromCharCode(num - 10 + 'A'.codeUnitAt(0));}}void strev(List<String> str) {int len = str.length;for (int i = 0; i < len ~/ 2; i++) {String temp = str[i];str[i] = str[len - i - 1];str[len - i - 1] = temp;}}String fromDeci(String res, int base, int inputNum) {int index = 0;while (inputNum > 0) {res += reVal(inputNum % base);inputNum = (inputNum / base).floor();}List<String> resList = res.split('');strev(resList);return resList.join('');}void main() {print("Konversi Sistem Bilangan dari Desimal");print("Number Base System Converter from Decimal");print("===========================================");stdout.write("Input Number : ");int inputNum = int.parse(stdin.readLineSync()!);stdout.write("Input Base : ");int base = int.parse(stdin.readLineSync()!);String res = "";print("$inputNum [$base] = ${fromDeci(res, base, inputNum)}");}
4. Dengan menggunakan GUI (Web + Desktop)
Sumber : Geeksforgeeks.org
Sama seperti di atas, hanya saja di sini menggunakan GUI dalam bentuk Web dan Desktop. Untuk Web, menggunakan HTML (Tanpa CSS) dan menggunakan Bahasa JavaScript dan PHP. Sedangkan, untuk Desktop menggunakan Java GUI dan Python GUI.
Input/Output (Web) :
Input/Output (Desktop GUI) :
Java GUI :
Python GUI (PyQt) :
Python GUI (Tkinter) :
1. JavaScript
<!DOCTYPE html><html><head><meta charset="UTF-8" /><title>Number Base System Converter from Decimal</title></head><body><h1>Konversi Sistem Bilangan dari Desimal<br />(Number Base System Converter from Decimal)</h1><hr /><form><label for="inputNum">Input Number:</label><input type="text" id="inputNum" name="inputNum" /><br /><br /><label for="base1">Input Base:</label><input type="text" id="base1" name="base1" /><br /><br /><input type="button" value="Convert" onclick="convert()" /><br /><br /></form><div id="result"></div><script>function reVal(num) {if (num >= 0 && num <= 9) return String.fromCharCode(num + 48);else return String.fromCharCode(num - 10 + 65);}function fromDeci(base1, inputNum) {let s = "";while (inputNum > 0) {s += reVal(inputNum % base1);inputNum = parseInt(inputNum / base1, 10);}let res = s.split("");res.reverse();return res.join("");}function convert() {let inputNum = document.getElementById("inputNum").value;let base1 = document.getElementById("base1").value;let output =inputNum + "[" + base1 + "] = " + fromDeci(base1, inputNum);document.getElementById("result").innerHTML = output;}</script></body></html>
2. PHP
<!DOCTYPE html><html><head><meta charset="UTF-8"><title>Number Base System Converter from Decimal</title></head><body><h1>Konversi Sistem Bilangan dari Desimal<br />(Number Base System Converter from Decimal)</h1><hr><form method="post"><label for="inputNum">Input Number:</label><input type="text" id="inputNum" name="inputNum"><br><br><label for="base1">Input Base:</label><input type="text" id="base1" name="base1"><br><br><input type="submit" name="convert" value="Convert"><br><br></form><div id="result"><?phpfunction reVal($num) {if ($num >= 0 && $num <= 9) return chr($num + 48);else return chr($num - 10 + 65);}function fromDeci($base1, $inputNum) {$s = "";while ($inputNum > 0) {$s .= reVal($inputNum % $base1);$inputNum = intval($inputNum / $base1, 10);}$res = str_split($s);$res = array_reverse($res);return implode("", $res);}if(isset($_POST['convert'])) {$inputNum = $_POST['inputNum'];$base1 = $_POST['base1'];$output = $inputNum . "[" . $base1 . "] = " . fromDeci($base1, $inputNum);echo $output;}?></div></body></html>
3. Java GUI
import javax.swing.*;import java.awt.event.*;public class NumberSystemConversionGUI extends JFrame {private JTextField inputNumField, baseField;private JLabel resultField;public NumberSystemConversionGUI() {setTitle("Number Base System Converter from Decimal");setSize(400, 250);setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);setLayout(null);JLabel inputNumLabel = new JLabel("Input Number:");inputNumLabel.setBounds(20, 20, 100, 25);add(inputNumLabel);inputNumField = new JTextField();inputNumField.setBounds(150, 20, 150, 25);add(inputNumField);JLabel baseLabel = new JLabel("Input Base:");baseLabel.setBounds(20, 60, 100, 25);add(baseLabel);baseField = new JTextField();baseField.setBounds(150, 60, 150, 25);add(baseField);JButton convertButton = new JButton("Convert");convertButton.setBounds(150, 100, 100, 25);convertButton.addActionListener(new ActionListener() {public void actionPerformed(ActionEvent e) {convert();}});add(convertButton);JLabel resultLabel = new JLabel("Result:");resultLabel.setBounds(20, 140, 100, 25);add(resultLabel);resultField = new JLabel("");resultField.setBounds(150, 140, 150, 25);add(resultField);}private char reVal(int num) {if (num >= 0 && num <= 9) {return (char) (num + 48);} else {return (char) (num - 10 + 65);}}private String fromDeci(int base, int inputNum) {StringBuilder res = new StringBuilder();while (inputNum > 0) {res.append(reVal(inputNum % base));inputNum /= base;}return res.reverse().toString();}private void convert() {int inputNum = Integer.parseInt(inputNumField.getText());int base = Integer.parseInt(baseField.getText());String result = fromDeci(base, inputNum);resultField.setText(result);}public static void main(String[] args) {SwingUtilities.invokeLater(new Runnable() {public void run() {new NumberSystemConversionGUI().setVisible(true);}});}}
4. Python GUI (PyQt5)
import sysfrom PyQt5.QtWidgets import QApplication, QMainWindow, QLabel, QLineEdit, QPushButtonclass NumberSystemConversionGUI(QMainWindow):def __init__(self):super().__init__()self.setWindowTitle("Number Base System Converter from Decimal")self.setGeometry(100, 100, 400, 200)self.inputNumLabel = QLabel("Input Number:", self)self.inputNumLabel.move(20, 20)self.inputNumField = QLineEdit(self)self.inputNumField.move(150, 20)self.baseLabel = QLabel("Input Base:", self)self.baseLabel.move(20, 60)self.baseField = QLineEdit(self)self.baseField.move(150, 60)self.convertButton = QPushButton("Convert", self)self.convertButton.move(150, 100)self.convertButton.clicked.connect(self.convert)self.resultLabel = QLabel("Result:", self)self.resultLabel.move(20, 140)self.resultField = QLabel(self)self.resultField.move(150, 140)self.resultField.resize(200, 30)def reVal(self, num):if num >= 0 and num <= 9:return chr(num + ord('0'))else:return chr(num - 10 + ord('A'))def fromDeci(self, base, inputNum):res = ""while inputNum > 0:res += self.reVal(inputNum % base)inputNum = int(inputNum / base)return res[::-1]def convert(self):inputNum = int(self.inputNumField.text())base = int(self.baseField.text())result = self.fromDeci(base, inputNum)self.resultField.setText(result)if __name__ == "__main__":app = QApplication(sys.argv)window = NumberSystemConversionGUI()window.show()sys.exit(app.exec_())
5. Python GUI (Tkinter)
import tkinter as tkdef reVal(num):if num >= 0 and num <= 9:return chr(num + ord('0'))else:return chr(num - 10 + ord('A'))def fromDeci(base, inputNum):res = ""while inputNum > 0:res += reVal(inputNum % base)inputNum = int(inputNum / base)return res[::-1]def convert():inputNum = int(inputNumField.get())base = int(baseField.get())result = fromDeci(base, inputNum)resultField.configure(text=result)root = tk.Tk()root.title("Number Base System Converter from Decimal")root.geometry("400x200")inputNumLabel = tk.Label(root, text="Input Number:")inputNumLabel.place(x=20, y=20)inputNumField = tk.Entry(root)inputNumField.place(x=150, y=20)baseLabel = tk.Label(root, text="Input Base:")baseLabel.place(x=20, y=60)baseField = tk.Entry(root)baseField.place(x=150, y=60)convertButton = tk.Button(root, text="Convert", command=convert)convertButton.place(x=150, y=100)resultLabel = tk.Label(root, text="Result:")resultLabel.place(x=20, y=140)resultField = tk.Label(root, text="")resultField.place(x=150, y=140)root.mainloop()
Untuk selengkapnya, silakan lihat di sini (GitHub Inzaghi's Dev).
Link Selengkapnya :
https://www.cs.utexas.edu/~byoung/cs429/slides2-bits-bytes-4up.pdf
https://bundet.com/d/861-pengertian-representasi-data
Untuk melihat Artikel tentang Jenis-jenis Pengkodean Karakter dalam Komputer, silakan lihat di sini.
Untuk melihat Tabel Perkalian dalam berbagai Sistem Bilangan (Multiplication Tables of various Bases), silakan lihat di sini atau lihat di sini (Dari The Dozenal Society of America). Atau, jika ingin melihat Konversi Sistem Bilangan dan juga Operasi Hitung dalam Bilangan Basis apapun, silakan klik di sini dan juga di sini.
Terima Kasih 😄😘👌👍 :)
Wassalamu‘alaikum wr. wb.

.png)






.jpg)
.jpg)
.jpg)

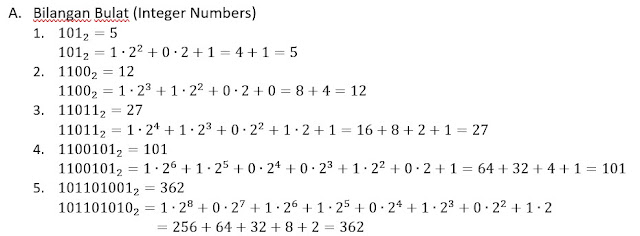



.jpg)
.jpg)
.jpg)

.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)






.jpg)
.jpg)
.jpg)

.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)









.jpg)
.jpg)
.jpg)

.jpg)
.jpg)
.jpg)

.jpg)
.jpg)
.jpg)





.jpg)

.jpg)
.jpg)
.jpg)

.jpg)
.jpg)
.jpg)

.jpg)
.jpg)
.jpg)







.jpg)
.jpg)
.jpg)









.jpg)
.jpg)
.jpg)









 mewakili pecahan 8/10, 1489/100, 24/100000, 1618/1000 dan 314159/100000, dan karenanya merupakan bilangan desimal.
mewakili pecahan 8/10, 1489/100, 24/100000, 1618/1000 dan 314159/100000, dan karenanya merupakan bilangan desimal.

.jpg)
.jpg)
.jpg)

.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)





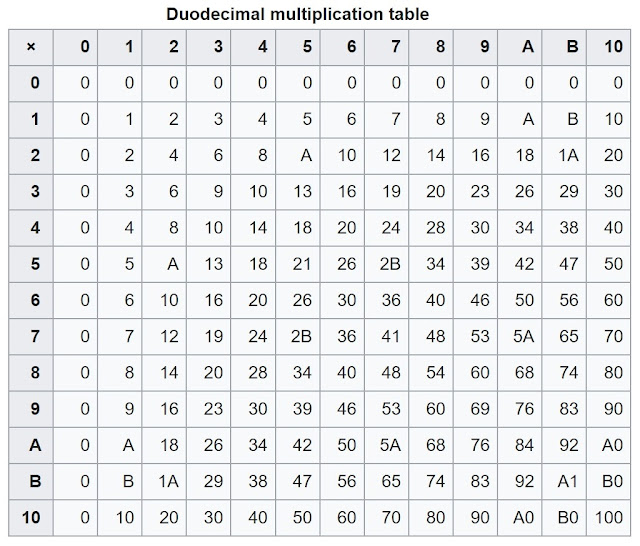






.jpg)
.jpg)
.jpg)

.jpg)
.jpg)
.jpg)

.jpg)
.jpg)
.jpg)

.jpg)
.jpg)
.jpg)





.png)
.png)
.jpg)



.png)
.png)










%20to%20Decimal.jpg)
%20to%20Decimal.jpg)
%20to%20Decimal.jpg)
%20to%20Decimal.jpg)
%20to%20Decimal.jpg)
%20to%20Decimal.jpg)
%20to%20Decimal.jpg)
%20to%20Decimal.jpg)
%20to%20Decimal.jpg)
%20to%20Decimal.jpg)
%5D.jpg)